题目内容
16．
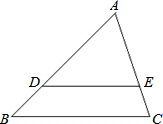如图，在△ABC中，点D、E分别是AB和AC上的点，DE∥BC，AD=3BD，S△ABC=48，求S四边形BCED．
分析 根据DE∥BC，于是得到△ADE∽△ABC，根据相似三角形的性质得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2，于是求得S△ADE=27，即可得到结论．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2，
∵AD=3BD，
∴$\frac{AD}{AB}$=$\frac{3}{4}$，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{9}{16}$，
∵S△ABC=48，
∴S△ADE=27，
∴S四边形BCED=S△ABC-S△ADE=48-27=21．
点评 此题考查了相似三角形的判定与性质．此题难度不大，注意掌握相似三角形面积的比等于相似比的平方定理的应用是解此题的关键．
练习册系列答案
相关题目
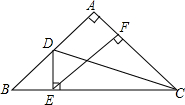如图所示，在等腰直角三角形ABC中，∠A=90°，∠ACB的平分线CD交AB于点D，DE⊥BC于点E．
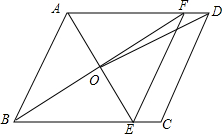如图，在平行四边形ABCD中，AE平分∠BAD交BC于点E，BF平分∠ABC交AD于点F，AE、BF交于点O，连接EF、OD．
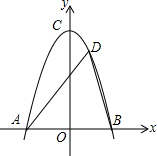如图，某公路隧道横截面为抛物线，其最大高度为8米，以隧道底部宽AB所在直线为x轴，以AB垂直平分线为y轴建立如图所示的平面直角坐标系，抛物线解析式为y=-$\frac{1}{2}{x}^{2}+b$，则隧道底部宽AB8米．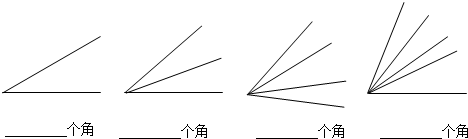
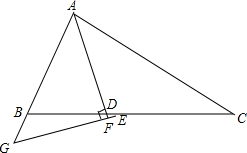已知：△ABC中，∠ABC=2∠ACB，AD是∠BAC的角平分线，E是BC的中点，过E作EF⊥AD交AD的延长线于F，交AB的延长线于G，求证：BD=2BG．
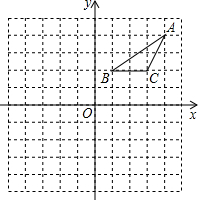在正方形网格中，建立如图所示的平面直角坐标系xOy，△ABC的三个顶点都在格点上，点A的坐标（4，4），请解答下列问题：