题目内容
7.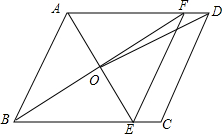 如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E,BF平分∠ABC交AD于点F,AE、BF交于点O,连接EF、OD.
如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E,BF平分∠ABC交AD于点F,AE、BF交于点O,连接EF、OD.(1)求证:四边形ABEF为菱形;
(2)若AB=4,AD=5,∠BCD=120°.求:tan∠ADO.
分析 (1)由平行四边形的性质和角平分线的定义得出∠BAE=∠AEB.证出AB=BE.同理AB=AF.得出AF=BE.证出四边形ABEF是平行四边形即可得出结论.
(2)作OH⊥AD于H,由菱形的性质得出AB=AF=4,∠ABC=60°,AO⊥BF,∠ABF=∠AFB=30°,由含30°角的直角三角形的性质得出AO=$\frac{1}{2}$AB=2,求出OH、DH,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE是角平分线,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
(2)解:作OH⊥AD于H,如图所示:
∵四边形ABEF是菱形,∠BCD=120°,AB=4,
∴AB=AF=4,∠ABC=60°,AO⊥BF,
∴∠ABF=∠AFB=30°,
∴AO=$\frac{1}{2}$AB=2,
∴OH=$\sqrt{3}$,AH=1,DH=AD-AH=4,
∴tan∠ADO=$\frac{OH}{DH}$=$\frac{\sqrt{3}}{4}$.
点评 本题考查了菱形的判定与性质、平行四边形的性质与判定、等腰三角形的判定、三角函数等知识;熟练掌握菱形的判定与性质是解决问题的关键,难度适中.

练习册系列答案
相关题目
17.下列语句正确的有( )个
①$\sqrt{256}$的平方根是±4;②一对相反数的立方根之和为0;
③平方根等于本身的数有1和0; ④$\sqrt{5a}$与$\sqrt{0.2a}$是同类二次根式.
①$\sqrt{256}$的平方根是±4;②一对相反数的立方根之和为0;
③平方根等于本身的数有1和0; ④$\sqrt{5a}$与$\sqrt{0.2a}$是同类二次根式.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15. 如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )
如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )
 如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )
如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
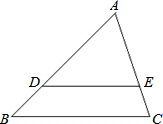 如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED.
如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED.