题目内容
8.顶角为120°的等腰三角形的底边长与底边上的高长的比是2$\sqrt{3}$:1,腰长与底边长的比是1:$\sqrt{3}$.分析 根据已知条件“等腰三角形的顶角为120°,底边上的中线长为4cm”画出图形,可求得底角为30°,设AD=x,由含30°的直角三角形的性质得出AB=2AD=2x,由勾股定理得出BD=$\sqrt{3}$x,得出BC=2BD=2$\sqrt{3}$x,即可得出结果.
解答 解: 如图所示,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,
如图所示,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,
∴∠B=30°,BD=CD=$\frac{1}{2}$BC,设AD=x,
则在Rt△ABD中,AB=2AD=2x,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{3}$x,
∴BC=2BD=2$\sqrt{3}$x,
∴BC:AD=2$\sqrt{3}$x:x=2$\sqrt{3}$:1,
AB:BC=2x:2$\sqrt{3}$x=1:$\sqrt{3}$.
故答案为:2$\sqrt{3}$:1,1:$\sqrt{3}$.
点评 本题考查了等腰三角形的性质、含30°角的直角三角形的性质、勾股定理;熟练掌握等腰三角形的性质,由含30°的直角三角形的性质得出AB=2AD是解决问题的关键.

练习册系列答案
相关题目
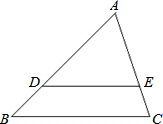 如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED.
如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED. 如图,A,B,C这三个点表示三个工厂,它们在同一个圆上,要建立一个供水站,使它到这三个工厂的距离相等,请找出供水站的位置.
如图,A,B,C这三个点表示三个工厂,它们在同一个圆上,要建立一个供水站,使它到这三个工厂的距离相等,请找出供水站的位置. 已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F.
已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F. 如图,在Rt△ABC中,∠ACB=90°,D为斜边的中点,点E、点F分别在直线CA、BC上,且DE⊥DF.
如图,在Rt△ABC中,∠ACB=90°,D为斜边的中点,点E、点F分别在直线CA、BC上,且DE⊥DF.