题目内容
4.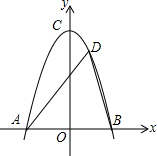 如图,某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-$\frac{1}{2}{x}^{2}+b$,则隧道底部宽AB8米.
如图,某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-$\frac{1}{2}{x}^{2}+b$,则隧道底部宽AB8米.
分析 由函数的解析式可求出A和B两点的坐标,进而求出AB的长.
解答 解:∵y=-$\frac{1}{2}{x}^{2}+b$,最大高度为8米,
∴b=8,
∴抛物线解析式为y=-$\frac{1}{2}$x2+8,
当y=0时,则0=-$\frac{1}{2}$x2+8,
解得:x=4或-4,
∴水面宽AB是4+4=8米.
故答案为:8.
点评 本题考查了二次函数的应用,比较简单,主要利用了待定系数法求二次函数解析式,二次函数图象上点的坐标特征,比较简单.

练习册系列答案
相关题目
15. 如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )
如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )
 如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )
如图,在边长为1的正方形网格中,△ABC的三边a,b,c的大小关系是( )| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
 如图,CD平分∠ACB,DE∥BC,∠AED=52°,求∠EDC的度数.
如图,CD平分∠ACB,DE∥BC,∠AED=52°,求∠EDC的度数.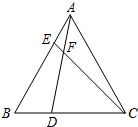 在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.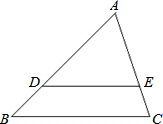 如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED.
如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED. 已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F.
已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F.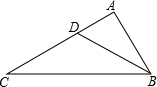 如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{2}$,那么$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$.
如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{2}$,那么$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$.