题目内容
1.在Rt△ABC中,∠C=90°,BC=3,AB=2$\sqrt{3}$,则∠B=30°.分析 根据题意和勾股定理得出AC,再根据在直角三角形中,30°角所对的直角边等于斜边的一半,即可得出答案.
解答 解:∵∠C=90°,BC=3,AB=2$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-{3}^{2}}$=$\sqrt{3}$,
∴AB=2AC,
∠B=30°;
故答案为:30°.
点评 此题考查了解直角三角形,用到的知识点是勾股定理、在直角三角形中,30°角所对的直角边等于斜边的一半,关键是根据题意得出AB=2AC.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
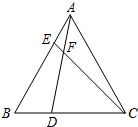 在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.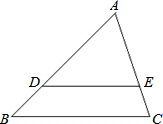 如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED.
如图,在△ABC中,点D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S四边形BCED. 已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F.
已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F.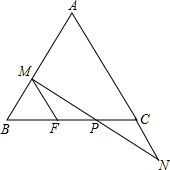 在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.
在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.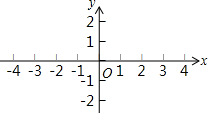 在平面直角坐标系中,已知点A(1,0),B(2,2),请在图中画出线段AB,并画出线段AB绕点O顺时针旋转90°后的图形.
在平面直角坐标系中,已知点A(1,0),B(2,2),请在图中画出线段AB,并画出线段AB绕点O顺时针旋转90°后的图形.