题目内容
14.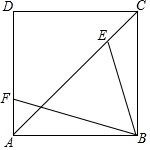 在面积为2的正方ABCD中,EF是线段AC,AD上的动点,且始终保持CE=AF.连接BE,BF.BE+BF是否有最小值?若有,请求出这个值;若无,请说明理由.
在面积为2的正方ABCD中,EF是线段AC,AD上的动点,且始终保持CE=AF.连接BE,BF.BE+BF是否有最小值?若有,请求出这个值;若无,请说明理由.
分析 BE+BF有最小值.过点C作CG⊥AC,使得CG=AB,由△ABF≌△CGE,推出BF=GE,推出BE+BF=BE+EG,因为BE+EG≥BG,所以BE+BF的最小值为BG的长.作BH⊥CG于H,易知△BCH是等腰直角三角形,由AB=$\sqrt{2}$,推出CH=BH=1,在Rt△BHG中,根据BG=$\sqrt{G{H}^{2}+B{H}^{2}}$即可解决问题.
解答 解:BE+BF有最小值.求法如下:
∵AC是正方形的对角线,
∴∠1=∠2=45°,∠DAB=90°,AB=BC,
过点C作CG⊥AC,使得CG=AB,
在△ABF和△CGE中,
$\left\{\begin{array}{l}{CE=AF}\\{∠BAF=∠GCE=90°}\\{AB=CG}\end{array}\right.$,
∴△ABF≌△CGE,
∴BF=GE,
∴BE+BF=BE+EG,
∵BE+EG≥BG,
∴BE+BF的最小值为BG的长.
作BH⊥CG于H,易知△BCH是等腰直角三角形,∵AB=$\sqrt{2}$,
∴CH=BH=1,
在Rt△BHG中,BG=$\sqrt{G{H}^{2}+B{H}^{2}}$=$\sqrt{{1}^{2}+(1+\sqrt{2})^{2}}$=$\sqrt{4+2\sqrt{2}}$.
点评 本题考查正方形的性质、全等三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.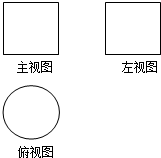 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
9.已知等腰三角形的一个内角为40°,则这个等腰三角形的底角为( )
| A. | 40° | B. | 100° | C. | 40°或100° | D. | 40°或70° |
19.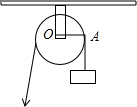 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )| A. | 5πcm | B. | 3πcm | C. | 2πcm | D. | πcm |
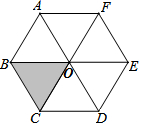 如图,六边形ABCDEF是由6个相同的等边三角形组成的,在这些三角形中,可以由△OBC平移得到的有( )个三角形.
如图,六边形ABCDEF是由6个相同的等边三角形组成的,在这些三角形中,可以由△OBC平移得到的有( )个三角形.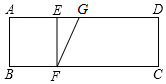 如图,在矩形ABCD中,AB=2,AD=6,E.F分别是线段AD,BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为4或4-2$\sqrt{2}$.
如图,在矩形ABCD中,AB=2,AD=6,E.F分别是线段AD,BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为4或4-2$\sqrt{2}$.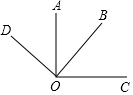 如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°.
如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°. 平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.