题目内容
5.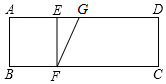 如图,在矩形ABCD中,AB=2,AD=6,E.F分别是线段AD,BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为4或4-2$\sqrt{2}$.
如图,在矩形ABCD中,AB=2,AD=6,E.F分别是线段AD,BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为4或4-2$\sqrt{2}$.
分析 当点P在AF上时,由翻折的性质可求得PF=FC=4,然后再求得正方形的对角线AF的长,从而可得到PA的长;当点P在BE上时,由正方形的性质可知BP为AF的垂直平分线,则AP=PF,由翻折的性质可求得PF=FC=4,故此可得到AP的值.
解答 解:如图1所示: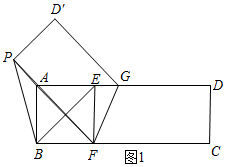
由翻折的性质可知PF=CF=4,
∵ABFE为正方形,边长为2,
∴AF=2$\sqrt{2}$.
∴PA=4-2$\sqrt{2}$.
如图2所示: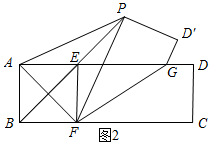
由翻折的性质可知PF=FC=4.
∵ABFE为正方形,
∴BE为AF的垂直平分线.
∴AP=PF=4.
故答案为:4或4-2$\sqrt{2}$.
点评 本题主要考查的是翻折的性质、正方形的性质的应用,根据题意画出符合题意的图形是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
15.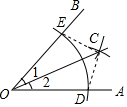 数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )
数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )
 数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )
数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )| A. | ∠1=∠2 | B. | S△OCE=S△OCD | C. | OD=CD | D. | OC垂直平分DE |
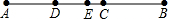 如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm.
如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm.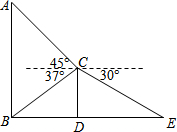 某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
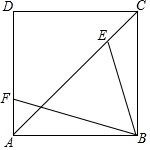 在面积为2的正方ABCD中,EF是线段AC,AD上的动点,且始终保持CE=AF.连接BE,BF.BE+BF是否有最小值?若有,请求出这个值;若无,请说明理由.
在面积为2的正方ABCD中,EF是线段AC,AD上的动点,且始终保持CE=AF.连接BE,BF.BE+BF是否有最小值?若有,请求出这个值;若无,请说明理由.