Question

2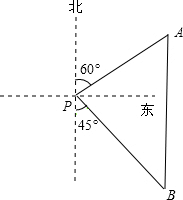．如图，一艘海轮位于灯塔P的北偏东60°方向，距灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，此时B处距离灯塔P有多远（结果取整数）．参考数值：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，$\sqrt{6}$≈2.4．

Answer 1

分析 作PC⊥AB于C，根据余弦的定义求出PC，再根据余弦的定义求出PB即可．

解答 解：作PC⊥AB于C，
由题意得，∠APC=30°，∠BPC=45°，AP=80海里，
在Rt△APC中，PC=AC•cos∠APC=40$\sqrt{3}$海里，
在Rt△BPC值，PB=$\frac{PC}{cos∠BPC}$=40$\sqrt{6}$≈96海里，
答：B处距离灯塔P96海里．

点评 本题考查的是解直角三角形的应用-方向角问题，正确标注方向角、熟记锐角三角函数的定义是解题的关键．