题目内容
17. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )| A. | (1,2) | B. | (1,1) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (2,1) |
分析 利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky),进而求出即可.
解答 解:∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,B(2,2),
∴点D的坐标为:(1,1).
故选:B.
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
相关题目
5.将二次函数y=2x2的图象向左平移2个单位,得到的新图象对应的函数表达式为( )
| A. | y=2x2+2 | B. | y=2(x+2)2 | C. | y=2x2-2 | D. | y=2(x-2)2 |
9. 如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
 如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )| A. | 0<x<2 | B. | x<0或x>2 | C. | x<0或x>4 | D. | 0<x<4 |
 如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m,求旗杆AB的高度.(结果精确到0.1m,参考数据$\sqrt{2}$≈1.41,sin52°≈0.79,tan52°≈1.28)
如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m,求旗杆AB的高度.(结果精确到0.1m,参考数据$\sqrt{2}$≈1.41,sin52°≈0.79,tan52°≈1.28)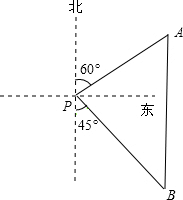 如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.
如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.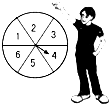 如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求: