题目内容
10. 如图,△ABC内接于圆O,若圆的半径是$\frac{5}{2}$,AB=3,求tanC的值.
如图,△ABC内接于圆O,若圆的半径是$\frac{5}{2}$,AB=3,求tanC的值.
分析 作直径AD,连接BD,根据圆周角定理得出∠ACB=∠ADB,在Rt△ABD中,求出∠ADB的正弦值即可.
解答  解:作直径AD,连接BD,
解:作直径AD,连接BD,
∵∠ACB和∠ADB都对弧AB,
∴∠ACB=∠ADB,
∵圆的半径是$\frac{5}{2}$,
∴AD=5,
∵AD为直径,
∴∠ABD=90°,
∴BD=$\sqrt{A{D}^{2}-A{B}^{2}}$=4,
∴tanC=tanD=$\frac{AB}{BD}$=$\frac{3}{4}$.
点评 本题考查了圆周角定理,三角形的外接圆和外心,解直角三角形的应用,关键是构造直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.将二次函数y=2x2的图象向左平移2个单位,得到的新图象对应的函数表达式为( )
| A. | y=2x2+2 | B. | y=2(x+2)2 | C. | y=2x2-2 | D. | y=2(x-2)2 |
15. 如图,在Rt△ABC中∠ACB=90°,斜边上的中线CF=8cm,DE是△ABC的中位线,则下列叙述中,正确的序号为( )
如图,在Rt△ABC中∠ACB=90°,斜边上的中线CF=8cm,DE是△ABC的中位线,则下列叙述中,正确的序号为( )
①S△ACF=S△BCF;②DE=8cm;③四边形CDFE是矩形;④S△ABC=2S△CDE.
 如图,在Rt△ABC中∠ACB=90°,斜边上的中线CF=8cm,DE是△ABC的中位线,则下列叙述中,正确的序号为( )
如图,在Rt△ABC中∠ACB=90°,斜边上的中线CF=8cm,DE是△ABC的中位线,则下列叙述中,正确的序号为( )①S△ACF=S△BCF;②DE=8cm;③四边形CDFE是矩形;④S△ABC=2S△CDE.
| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
19.以下各组线段为边不能组成三角形的是( )
| A. | 4,3,3 | B. | 1,5,6 | C. | 2,5,4 | D. | 5,8,4 |
17.某商人在一次买卖中均以180元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )
| A. | 赚24元 | B. | 赔24元 | C. | 不赚不赔 | D. | 无法确定 |
 如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点
如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点 如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1). 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离是100$\sqrt{3}$m.(结果保留要有号,不取近似值)
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离是100$\sqrt{3}$m.(结果保留要有号,不取近似值)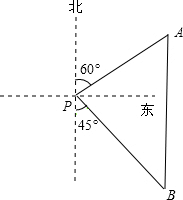 如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.
如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.