题目内容
14. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于( )
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
分析 根据翻折的性质可知:AC=AE=6,CD=DE,设CD=DE=x,在RT△DEB中利用勾股定理解决.
解答 解: 在RT△ABC中,∵AC=6,BC=8,
在RT△ABC中,∵AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
△ADE是由△ACD翻折,
∴AC=AE=6,EB=AB-AE=10-6=4,
设CD=DE=x,
在RT△DEB中,∵DEDE2+EB2=DB2,
∴x2+42=(8-x)2
∴x=3,
∴CD=3.
故选B.
点评 本题考查翻折的性质、勾股定理,利用翻折不变性是解决问题的关键,学会转化的思想去思考问题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
5.将二次函数y=2x2的图象向左平移2个单位,得到的新图象对应的函数表达式为( )
| A. | y=2x2+2 | B. | y=2(x+2)2 | C. | y=2x2-2 | D. | y=2(x-2)2 |
9. 如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
 如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )| A. | 0<x<2 | B. | x<0或x>2 | C. | x<0或x>4 | D. | 0<x<4 |
19.以下各组线段为边不能组成三角形的是( )
| A. | 4,3,3 | B. | 1,5,6 | C. | 2,5,4 | D. | 5,8,4 |
2. 如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )| A. | 美 | B. | 丽 | C. | 莱 | D. | 山 |
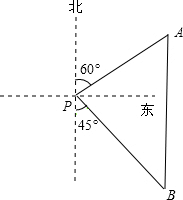 如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.
如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.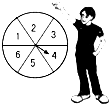 如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求: