题目内容
9.将一个正三角形纸片在图1中分成四个全等的小正三角形,再将其中的一个按同样的方法分成四个更小的正三角形,得到图2 …以此类推.
(1)图2中有9个正三角形,图5中有21个正三角形;
(2)图n中有4n+1个正三角形;
(3)能得到246个正三角形吗?说明理由.
分析 (1)根据图形变化得出图n中有4n+1个正三角形,代入n=2,n=5即可;
(2)根据图形变化得出图n中有4n+1个正三角形;
(3)令令4n+1=246,如果解出n为整数即可以,如果不是整数则不可以.
解答 解:根据图形的变化,可知:没往后一个图形增添4个正三角形,图1中正三角形的个数为4+1=5个,
图n中有4n+1个正三角形.
(1)令n=2,可得4×2+1=9(个);
令n=5,可得4×5+1=21(个).
故答案为:9;21.
(2)图n中有4n+1个正三角形,
故答案为:4n+1.
(3)∵令4n+1=246,解得n=61…1,有余数,
∴不能得到246个正三角形.
点评 本题考查了图形的变化,解题的关键是:根据图形的变化,找出“图n中有4n+1个正三角形”这一结论.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
2. 如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字相对的面上的字是( )| A. | 美 | B. | 丽 | C. | 莱 | D. | 山 |
17.某商人在一次买卖中均以180元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )
| A. | 赚24元 | B. | 赔24元 | C. | 不赚不赔 | D. | 无法确定 |
14.某地去年棉花产量为n吨,今年棉花产量增产30%,则今年该地棉花的产量为( )
| A. | (1+30%)n吨 | B. | (1-30%)n吨 | C. | 30%n吨 | D. | (n+30%)吨 |
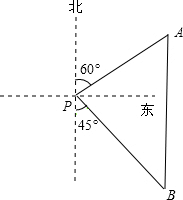 如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.
如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4. 某校七年级(一)班共有50名学生,分别参加了写作、数学、英语、篮球及摄影兴趣小组,每个学生必须参加且只能参加其中一种,请根据如图所示的扇形统计图.求:
某校七年级(一)班共有50名学生,分别参加了写作、数学、英语、篮球及摄影兴趣小组,每个学生必须参加且只能参加其中一种,请根据如图所示的扇形统计图.求: