题目内容
7.A、B两乡分别由大米200吨、300吨.现将这些大米运至C、D两个粮站储存.已知C粮站可储存240吨,D粮站可储存260吨,从A乡运往C、D两处的费用分别为每吨20元和25元,B乡运往C、D两处的费用分别为每吨15元和18元.设A乡运往C粮站大米x吨.A、B两乡运往两个粮站的运费分别为yA、yB元.(1)请填写下表,并求出yA、yB与x的关系式:
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200吨 | |
| B乡 | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
(3)若B乡比较困难,最多只能承受4830元费用,这种情况下,运输方案如何确定才能使总运费最少?最少的费用是多少?
分析 (1)结合已知完善表格,再根据运费=运输单价×数量,得出yA、yB与x的关系式;
(2)令yA=yB,找出二者运费相等的x,以此为界分成三种情况;
(3)由B乡运费最多为4830元,找出x的取值范围,再根据yA+yB的单调性,即可得知当x取什么值时,总运费最低.
解答 解:(1)根据已知补充表格如下:
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200-x吨 | 200吨 |
| B乡 | 240-x吨 | x+60吨 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
B乡运往两个粮站的运费yB=15×(240-x)+18×(x+60)=3x+4680(0≤x≤200).
(2)令yA=yB,即-5x+5000=3x+4680,
解得:x=40.
故当x<40时,B乡运费少;当x=40时,A、B两乡运费一样多;当x>40时,A乡运费少.
(3)令yB≤4830,即3x+4680≤4830,
解得:x≤50.
总运费y=yA+yB=-5x+5000+3x+4680=-2x+9680,
∵-2<0,
∴y=-2x+9680单调递减.
故当x=50时,总运费最低,最低费用为9580元.
点评 本题考查了一次函数的单调性以及解一元一次不等式,解题的关键是:(1)由运费=运输单价×数量结合表格得出结论;(2)令yA=yB得出x,在分类探讨;(3)由一元一次不等式找出x的取值范围,再根据单调性求最值.本题属于基础题,难度不大,做该类型题目时,要明确条件中的数量关系,找准关系式.

练习册系列答案
相关题目
19.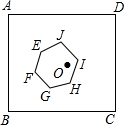 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{3+2\sqrt{3}}{6}$ | D. | $\frac{3-2\sqrt{3}}{6}$ |
 如图,已知a⊥b,b⊥c,c⊥d,求证:a⊥d.
如图,已知a⊥b,b⊥c,c⊥d,求证:a⊥d.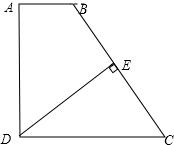 如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系.
如图,在直角梯形ABCD中,已知AB∥DC,DE⊥BC,E是BC的中点,探究AB,DC,AD的关系. 如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.
如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.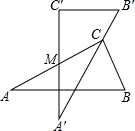 两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.
两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C,如图所示.已知AC=6,则这两块直角三角板顶点A、A′之间的距离等于3.