题目内容
2. 如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.
如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.
分析 首先连接BE,由折叠的性质可得:AB=BE,即可得$\widehat{AB}$=$\widehat{BE}$,然后由圆周角定理,∠BAE和∠BEA的度数,继而求得∠ABE的度数.
解答 解:连接AE,
由折叠的性质可得:AB=BE,
∴$\widehat{AB}$=$\widehat{BE}$,
∴∠BAE=∠BEA=∠C=50°,
∴∠ABE=180°-50°-50°=80°.
故答案为:80°.
点评 此题考查了圆周角定理,折叠的性质以及三角形内角和定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
7.A、B两乡分别由大米200吨、300吨.现将这些大米运至C、D两个粮站储存.已知C粮站可储存240吨,D粮站可储存260吨,从A乡运往C、D两处的费用分别为每吨20元和25元,B乡运往C、D两处的费用分别为每吨15元和18元.设A乡运往C粮站大米x吨.A、B两乡运往两个粮站的运费分别为yA、yB元.
(1)请填写下表,并求出yA、yB与x的关系式:
(2)试讨论A、B乡中,哪一个的运费较少;
(3)若B乡比较困难,最多只能承受4830元费用,这种情况下,运输方案如何确定才能使总运费最少?最少的费用是多少?
(1)请填写下表,并求出yA、yB与x的关系式:
| C站 | D站 | 总计 | |
| A乡 | x吨 | 200吨 | |
| B乡 | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
(3)若B乡比较困难,最多只能承受4830元费用,这种情况下,运输方案如何确定才能使总运费最少?最少的费用是多少?
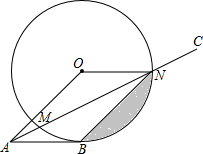 如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.
如图,AB切⊙O于点B,AC交⊙O于点M、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm. 如图,在四边形ABCD中,AB=AC,∠ABC=60°,∠ADC=30°,求证:DB2=DC2+DA2.
如图,在四边形ABCD中,AB=AC,∠ABC=60°,∠ADC=30°,求证:DB2=DC2+DA2.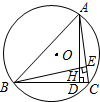 如图,△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H.若BC=6,AH=4,则⊙O的半径为$\sqrt{13}$.
如图,△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H.若BC=6,AH=4,则⊙O的半径为$\sqrt{13}$. 如图,△ABC中,BF是高,延长CB至点D,使BD=BA,连接AD,过点D作DE⊥AB交AB的延长线于点E,当AF=BE,∠CAD=96°时,∠C=56°.
如图,△ABC中,BF是高,延长CB至点D,使BD=BA,连接AD,过点D作DE⊥AB交AB的延长线于点E,当AF=BE,∠CAD=96°时,∠C=56°.