题目内容
9.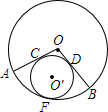 如图,在⊙O中,圆心角∠AOB=120°,⊙O′与OA、OB相切于点C、D,与$\widehat{AB}$相切于F,求$\widehat{AB}$的长与⊙O′的周长的比.
如图,在⊙O中,圆心角∠AOB=120°,⊙O′与OA、OB相切于点C、D,与$\widehat{AB}$相切于F,求$\widehat{AB}$的长与⊙O′的周长的比.
分析 如图连接OF,CO′,设O′F=O′C=r,在RT△OO′C中求出OO′,利用弧长公式、圆周长公式即可计算.
解答 解:如图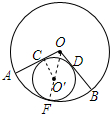 ,连接OF,CO′,设O′F=O′C=r,
,连接OF,CO′,设O′F=O′C=r,
∵∠AOB=120°,
OA、OB是⊙O′的切线,
∴∠AOO′=$\frac{1}{2}$∠AOB=60°,∠OCO′=90°,
∴∠CO′O=30°,
∴OO′=2CO,CO=$\frac{\sqrt{3}}{3}$r,OO′=$\frac{2\sqrt{3}}{3}$,OF=(1+$\frac{2\sqrt{3}}{3}$)r,
∴$\widehat{AB}$的长;⊙O′的周长=$\frac{120π(1+\frac{2\sqrt{3}}{3})r}{180}$:2πr=(3+2$\sqrt{3}$):9.
点评 本题考查切线的性质、弧长公式、圆的周长公式、直角三角形30度角的性质等知识,解题的关键是记住弧长公式、圆的周长公式,学会设未知数,表示相应的线段,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列能判定四边形是平行四边形的有( )
| A. | 一组对边相等,一组对角也相等 | |
| B. | 一组对边相等,一条对角线被另一条平分 | |
| C. | 一组对角相等,一条对角线被另一条平分 | |
| D. | 一组对角相等,过这组对角的顶点的对角线平分另一条对角线 |
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.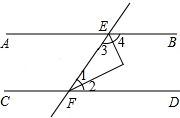 如图,直线AB,CD被EF所截,∠1=∠2,∠3=∠4,∠1+∠3=90°,那么AB与CD平行吗?为什么?
如图,直线AB,CD被EF所截,∠1=∠2,∠3=∠4,∠1+∠3=90°,那么AB与CD平行吗?为什么?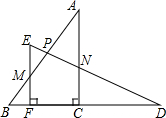 将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.
将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.
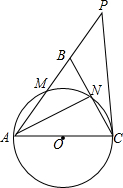 如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.