题目内容
4.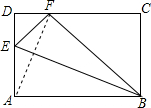 如图,矩形ABCD中,AB>AD,E在AD上,将△ABE沿BE折叠后,A点落在CD上,记为点F.
如图,矩形ABCD中,AB>AD,E在AD上,将△ABE沿BE折叠后,A点落在CD上,记为点F.(1)用尺规作出点E、F;
(2)若AB=5,AD=3,求折痕BE的长.
分析 (1)根据题意作图即可;
(2)在△DEF中利用勾股定理可求得DF的长,证明Rt△ADF∽Rt△BAE,利用相似三角形的性质可求得BF的长,在△BEF中利用勾股定理可求得BE的长.
解答 解:(1)作法: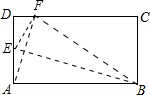
①作BF=BA交CD于F.
②连BF作∠ABF的平分线,则点E、F为所求.
(2)连接EF
由条件知:Rt△ABE≌Rt△FBE
∴EF=AE
又∵AE=5,DE=3,∠D=90°
∴DF=$\sqrt{{5}^{2}-{3}^{2}}$=4
又∵BE⊥AF
∴Rt△ADF∽Rt△BAE
∴$\frac{AD}{AB}=\frac{DF}{AE}$
∴AB=$\frac{AD•AE}{DF}$=$\frac{8×5}{4}$=10.
∴BE=$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$.
点评 考查了翻折变换(折叠问题)、勾股定理、相似三角形的性质,利用翻折的性质找出图形中的等量是解题的关键.

练习册系列答案
相关题目
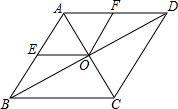 平行四边形ABCD的对角线AC,BD相交于点O,AE=EB,OF=$\frac{1}{2}$CD,求证:四边形AEOF为平行四边形.
平行四边形ABCD的对角线AC,BD相交于点O,AE=EB,OF=$\frac{1}{2}$CD,求证:四边形AEOF为平行四边形. 如图,已知AB为⊙O的直径,CE切⊙O于C点,过B点的直线BD交直线CE于D点,如果BC平分∠ABD.求证:BD⊥CE.
如图,已知AB为⊙O的直径,CE切⊙O于C点,过B点的直线BD交直线CE于D点,如果BC平分∠ABD.求证:BD⊥CE.