题目内容
14.将下列各式分解因式(1)x2y-2xy2
(2)t2-16
(3)a2-4a+4
(4)3x-12x3
(5)2x2+2x+$\frac{1}{2}$
(6)2m(a-b)-3n(b-a)
(7)x2-2xy+y2-1
(8)(a2+b2)2-4a2b2
(9)a2-b2-4a+4b.
分析 (1)原式提取公因式即可得到结果;
(2)原式利用平方差公式化简即可得到结果;
(3)原式利用完全平方公式分解即可;
(4)原式提取公因式即可得到结果;
(5)原式提取2,再利用完全平方公式分解即可;
(6)原式变形后,提取公因式即可得到结果;
(7)原式前三项结合,利用完全平方公式变形,再利用平方差公式分解即可;
(8)原式利用平方差公式及完全平方公式分解即可;
(9)原式两项两项结合,利用平方差公式分解,提取公因式即可.
解答 解:(1)原式=xy(x-2y);
(2)原式=(t+4)(t-4);
(3)原式=(a-2)2;
(4)原式=3x(1-4x2)=3x(1+2x)(1-2x);
(5)原式=2(x2+x+$\frac{1}{4}$)=2(x+$\frac{1}{2}$)2;
(6)原式=2m(a-b)+3n(a-b)=(2m+3n)(a-b);
(7)原式=(x-y)2-1=(x-y+1)(x-y-1);
(8)原式=(a2+b2+2ab)(a2+b2-2ab)=(a+b)2(a-b)2;
(9)原式=(a+b)(a-b)-4(a-b)=(a-b)(a+b-4).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.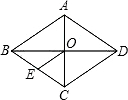 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
6. 如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
 如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )| A. | ∠1=∠2 | B. | AC=CA | C. | AC=BC | D. | ∠D=∠B |
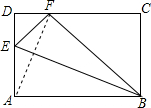 如图,矩形ABCD中,AB>AD,E在AD上,将△ABE沿BE折叠后,A点落在CD上,记为点F.
如图,矩形ABCD中,AB>AD,E在AD上,将△ABE沿BE折叠后,A点落在CD上,记为点F.