题目内容
12．
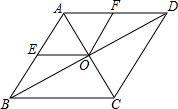平行四边形ABCD的对角线AC，BD相交于点O，AE=EB，OF=$\frac{1}{2}$CD，求证：四边形AEOF为平行四边形．
分析 由平行四边形的性质得出AB=CD，AB∥CD，OA=OC，证出OF为△ACD的中位线，得出OF∥CD，因此AE∥OF，且AE=OF，即可得出结论．
解答 证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，OA=OC，
∵OF=$\frac{1}{2}$CD，
∴OF为△ACD的中位线，
∴OF∥CD，
∵AE=EB=$\frac{1}{2}$AB，
∴AE∥OF，且AE=OF，
∴四边形AEOF为平行四边形 （一组对边平行且相等的四边形是平行四边形）．
点评 本题考查了平行四边形的判定与性质、三角形中位线定理；熟练掌握平行四边形的判定与性质，并能进行推理论证是解决问题的关键．
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
如图：在△ABC中，BD、CE分别是△ABC边AC、AB上的高，直线BD、CE相交于H．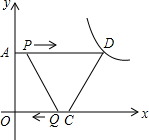
如图，在平面直角坐标系中，已知点D为函数y=$\frac{18}{x}$（x＞0）上 的一点，四边形ABCD是直角梯形（点B在坐标原点处），AD∥BC，∠B=90°，A（0，3），C（4，0），点P从A出发，以4个单位/秒的速度沿直线AD向右运动，点Q从点C同时出发，以2个单位/秒的速度沿直线CB向左运动．
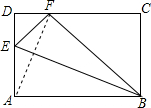如图，矩形ABCD中，AB＞AD，E在AD上，将△ABE沿BE折叠后，A点落在CD上，记为点F．