题目内容
13．计算：$\frac{1}{a（a+1）}$+$\frac{1}{（a+1）（a+2）}$+…+$\frac{1}{（a+2009）（a+2010）}$．分析 利用$\frac{1}{a（a+1）}$=$\frac{1}{a}$-$\frac{1}{a+1}$，$\frac{1}{（a+1）（a+2）}$=$\frac{1}{a+1}$-$\frac{1}{a+2}$…进而化简求出即可．
解答 解：$\frac{1}{a（a+1）}$+$\frac{1}{（a+1）（a+2）}$+…+$\frac{1}{（a+2009）（a+2010）}$
=$\frac{1}{a}$-$\frac{1}{a+1}$+$\frac{1}{a+1}$-$\frac{1}{a+2}$+…+$\frac{1}{a+2009}$-$\frac{1}{a+2010}$
=$\frac{1}{a}$-$\frac{1}{a+2010}$
=$\frac{2010}{{a}^{2}+2010a}$．
点评 此题主要考查了分式的加减运算，正确将原式变形化简是解题关键．
练习册系列答案
相关题目
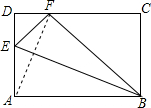如图，矩形ABCD中，AB＞AD，E在AD上，将△ABE沿BE折叠后，A点落在CD上，记为点F．