题目内容
7.为了解学生的课余生活,某中学在全校范围内随机抽取部分学生进行问卷调查,问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类.调查后将数据绘制成扇形统计图和条形统计图(如图所示).(1)请根据所给的扇形图和条形图,直接填写出扇形图中缺失的数据,并把条形图补充完整;
(2)在扇形统计图中,音乐类选项所在的扇形的圆心角的大小为57.6°;
(3)这所中学共有学生1200人,求喜欢音乐和美术类的课余生活共有多少人?
(4)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率.
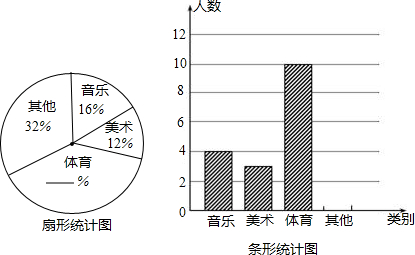
分析 (1)根据扇形统计图所给的数据,直接进行相减即可求出体育所占的百分比,再根据抽取体育的人数,即可求出抽取的总人数,再根据其他类所占的比例,即可求出答案.
(2)音乐类人数所占百分比乘以360°可得音乐类选项所在的扇形的圆心角的大小.
(3)根据学生中最喜欢音乐和美术类的学生所占的百分比,再乘以总数即可求出答案.
(4)首先由(1)可得音乐类的有4人,选择美术类的有3人.然后记选择音乐类的4人分别是A1,A2,A3,小丁;选择美术类的3人分别是B1,B2,小李.则可根据题意画出树状图,由树状图求得所有等可能的结果与小丁和小李恰好都被选中的情况,再利用概率公式求解即可求得答案.
解答 解:(1)根据题意得:
体育所占的百分比是:1-32%-12%-16%=40%,
抽取的总人数是:10÷40%=25(人),
其他类的人数是:25×32%=8(人).
如图所示: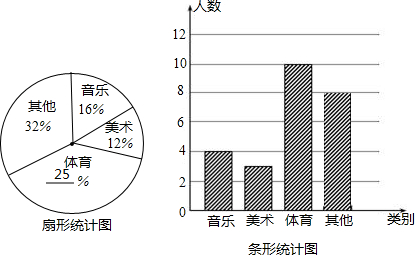
(2)音乐类选项所在的扇形的圆心角的大小为360°×16%=57.6°,
故答案为:57.6°.
(3)1200×(16%+12%)=336(人),
答:喜欢音乐和美术类的课余生活共有336人.
(4)选择音乐类的有4人,选择美术类的有3人,记选择音乐类的4人分别为A1、A2、A3、小丁,选择美术类的3人分别是B1、B2、小李,
列表如下:
| A1 | A2 | A3 | 小丁 | |
| B1 | A1、B1 | A2、B1 | A3、B1 | 小丁、B1 |
| B2 | A1、B2 | A2、B2 | A3、B2 | 小丁、B2 |
| 小李 | A1、小李 | A2、小李 | A3、小李 | 小丁、小李 |
∴小丁和小李恰好都被选中的概率为$\frac{1}{12}$.
点评 此题考查了条形统计图、扇形统计图与用列表法或树状图法求概率的知识.解题的关键是读懂题意,从图中得到必要的信息,注意掌握概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15. 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )| A. | 24 | B. | 12 | C. | 6 | D. | 8 |
16.下列点中,位于函数y=$\frac{2}{x}$图象上的是( )
| A. | (1,2) | B. | (1,$\frac{1}{2}$) | C. | (1,1) | D. | (2,$\frac{1}{2}$) |
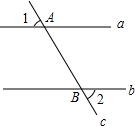 如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=60°.
如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=60°.
 为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过50分钟后教室内的空气才能达到安全要求.
为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过50分钟后教室内的空气才能达到安全要求.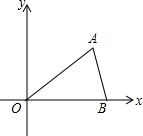 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A. 如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.