题目内容
3.分解因式:(1)16x2-1
(2)8ab3c2-32a2b2c+ab2c
(3)2m2-8n2
(4)4(a-y)+25x2(y-a)
(5)4q(1-p)3+2(p-1)2
(6)x2-2xy+y2+2x-2y-3.
分析 (1)直接利用平方差公式分解因式;
(2)利用提公因式法分解因式;
(3)先提公因式2,再利用利用平方差公式分解因式;
(4)将y-a提负号化成-(a-y),提公因式后再利用平方差公式分解因式;
(5)利用提公因式2(1-p)2分解因式,注意(p-1)2=(1-p)2;
(6)先配方,再利用公式法分解因式,注意要把x-y看成是一个整体.
解答 解:(1)16x2-1=(4x+1)(4x-1);
(2)8ab3c2-32a2b2c+ab2c,
=ab2c(8bc-32a+1);
(3)2m2-8n2=2(m+2n)(m-2n);
(4)4(a-y)+25x2(y-a),
=(a-y)(4-25x2),
=(a-y)(2+5y)(2-5y);
(5)4q(1-p)3+2(p-1)2,
=2(1-p)2[2q(1-p)+1],
=2(1-p)2(2q-2qp+1);
(6)x2-2xy+y2+2x-2y-3,
=(x-y)2+2(x-y)-3,
=(x-y-1)(x-y+3).
点评 本题考查了分组分解法、提公因式法、公式法进行因式分解;分组分解法是因式分解中的一个难点,恰当地采用两两分组或三一分组是关键;本题前三项可组成完全平方公式,可把前三项分为一组;在利用提公因式法分解因式时要注意公因式要一次性全部提出,不要遗漏.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.如图所示正三棱柱的主视图是( )


| A. |  | B. |  | C. |  | D. |  |
15. 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )
如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=12,则HE等于( )| A. | 24 | B. | 12 | C. | 6 | D. | 8 |
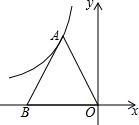 如图,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象过等边三角形AOB的顶点A(-1,$\sqrt{3}$),已知点B在x轴上.
如图,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象过等边三角形AOB的顶点A(-1,$\sqrt{3}$),已知点B在x轴上. 为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过50分钟后教室内的空气才能达到安全要求.
为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(分钟)的函数关系如图所示.已知,药物燃烧阶段,y与x成正比例,燃完后y与x成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体才能无毒害作用.那么从消毒开始,经过50分钟后教室内的空气才能达到安全要求. 如图,矩形ABCD被分成四部分.其中△CEF、△ABE、△ADF的面积分别是3、4、5,则△AEF的面积为8.
如图,矩形ABCD被分成四部分.其中△CEF、△ABE、△ADF的面积分别是3、4、5,则△AEF的面积为8.