题目内容
7.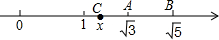 如图,数轴上与$\sqrt{3}、\sqrt{5}$对应的点分别是A,B,点C也在数轴上,且AB=AC,设点C表示的数为x
如图,数轴上与$\sqrt{3}、\sqrt{5}$对应的点分别是A,B,点C也在数轴上,且AB=AC,设点C表示的数为x(1)求x的值;
(2)计算|x-$\sqrt{3}$|$+\frac{6}{x+\sqrt{5}}$.
分析 (1)根据数轴上两点间距离公式表示出AB、AC的长,列出方程可求得x的值;
(2)将x的值代入计算可得.
解答 解:(1)设C点表示x,
∵数轴上A、B两点表示的数分别为$\sqrt{3}$和$\sqrt{5}$,且AB=AC,
∴$\sqrt{3}$-x=$\sqrt{5}$-$\sqrt{3}$,解得x=2$\sqrt{3}$-$\sqrt{5}$;
(2)原式=|2$\sqrt{3}$-$\sqrt{5}$-$\sqrt{3}$|+$\frac{6}{2\sqrt{3}-\sqrt{5}+\sqrt{5}}$
=$\sqrt{5}$-$\sqrt{3}$+$\sqrt{3}$
=$\sqrt{5}$.
点评 此题主要考查了利用数形结合的思想求出数轴两点之间的距离,解决问题的关键是根据已知条件求出a的值.

练习册系列答案
相关题目
2.在平面直角坐标系中,正方形OABC的顶点A坐标为(2,1),点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
| A. | -$\sqrt{5}$ | B. | -2 | C. | 2 | D. | $\sqrt{5}$ |
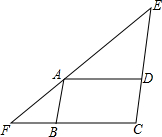 如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF.
如图,在△EFC中,点A是EF上一点,且AD∥CF,AB∥CE,∠EAD=∠BAF. 已知?ABCD的两条对角线相交于点O,AB=5,BC=5,BD=8,求?ABCD的周长与面积.
已知?ABCD的两条对角线相交于点O,AB=5,BC=5,BD=8,求?ABCD的周长与面积.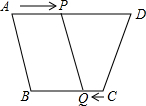 如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形?
如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形? 如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,
如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,