题目内容
12.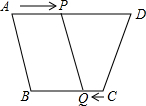 如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形?
如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形?
分析 设点P由A向D运动t秒,则AP=tcm,CQ=2tcm,再由BC长可表示出BQ=12-2t,根据平行四边形的判定可得AP平行且等于BQ时四边形APQB恰好为平行四边形,因此12-2t=t,再解即可.
解答 解:设点P由A向D运动t秒,则AP=tcm,CQ=2tcm.
∵BC=12,
∴BQ=12-2t,
若四边形ABQP为平行四边形,则须AP平行且等于BQ.
∴12-2t=t,
∴t=4,
∴4s后四边形ABQP成为平行四边形.
点评 此题主要考查了平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
4.已知直线y=-x+4与x轴、y轴分别交于A,B两点,与反比例函数y=$\frac{k}{x}$(k>0)的图象交于C,D两点,若AB=$\sqrt{2}$CD,则k的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
 已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求:
已知一次函数y=kx与反比例函数y=$\frac{3}{x}$的图象都经过点A(m,1).求: 如图,AB=DC.
如图,AB=DC.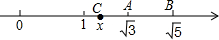 如图,数轴上与$\sqrt{3}、\sqrt{5}$对应的点分别是A,B,点C也在数轴上,且AB=AC,设点C表示的数为x
如图,数轴上与$\sqrt{3}、\sqrt{5}$对应的点分别是A,B,点C也在数轴上,且AB=AC,设点C表示的数为x 如图,分别以△ABC的三边为边,在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR,连接PA,AQ,QR,RP,那么四边形PRQA是平行四边形吗?证明你的结论.
如图,分别以△ABC的三边为边,在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR,连接PA,AQ,QR,RP,那么四边形PRQA是平行四边形吗?证明你的结论.