题目内容
8.如图,在平面直角坐标系xOy中,直线y=x-3与x轴相交于点B、y轴相交于点C,过点B、C的抛物线y=-x2+bx+c与x轴交于另一点A,顶点为D点.(1)求tan∠OCA的值;
(2)若点P为抛物线上x轴上方一点,且∠DAP=∠ACB,求点P的坐标;
(3)若点Q为抛物线y=-x2+bx+c对称轴上一动点,试探究当点Q为何位置时∠OQC最大,请求出点Q的坐标及sin∠OQC的值.
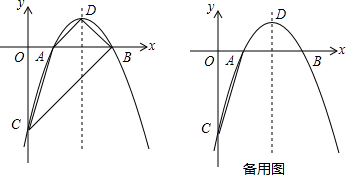
分析 (1)可先求出点B、C的坐标,然后用待定系数法求出抛物线的解析式,然后求出点A的坐标,就可解决问题;
(2)过点P作PE⊥x轴于E,如图1,易证∠DAH=∠OCB=45°,由∠DAP=∠ACB可得∠PAB=∠OCA,然后利用(1)中的结论运用三角函数就可解决问题;
(3)运用圆周角定理和三角形的外角的性质可得:当点Q在线段OC的垂直平分线上时,∠OQC最大,如图2①,过点O作OG⊥CQ于G,如图2②,运用勾股定理可求出OQ、CQ,然后运用面积法求出OG,问题得以解决.
解答 解:(1)∵点B、C分别是直线y=x-3与x轴、y轴的交点,
∴点B(3,0),点C(0,-3).
把点B(3,0),点C(0,-3)代入y=-x2+bx+c,得
$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=4}\\{c=-3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+4x-3.
令y=0,得-x2+4x-3=0,
解得x1=1,x2=3,
∴点A(1,0),OA=1,
∴tan∠OCA=$\frac{OA}{OC}$=$\frac{1}{3}$;
(2)过点P作PE⊥x轴于E,如图1,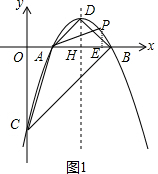
设点P的坐标为(x,-x2+4x-3),
则PE=-x2+4x-3,AE=x-1.
令y=0,得-x2+4x-3=0,
解得x1=1,x2=3,
∴B(3,0),
∴OB=OC=3.
∵∠BOC=90°,
∴∠OCB=45°.
由y=-x2+4x-3=-(x-2)2+1得,
顶点D(2,1),对称轴为x=2,
∴AH=DH=1.
∵∠DHA=90°,
∴∠DAH=45°,
∴∠DAH=∠OCB=45°.
∵∠DAP=∠ACB,
∴∠PAB=∠OCA,
∴tan∠PAB=tan∠OCA=$\frac{1}{3}$,
∴$\frac{PE}{AE}$=$\frac{-{x}^{2}+4x-3}{x-1}$=-$\frac{(x-1)(x-3)}{x-1}$=-(x-3)=$\frac{1}{3}$,
解得:x=$\frac{8}{3}$.
此时-x2+4x-3=-($\frac{8}{3}$)2+4×$\frac{8}{3}$-3=$\frac{5}{9}$,
则点P($\frac{8}{3}$,$\frac{5}{9}$);
(3)当点Q在线段OC的垂直平分线上时,∠OQC最大,如图2①,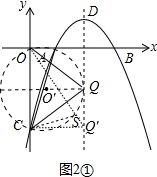
理由:在对称轴上任取一点Q′,连接OQ′,CQ′,
设OQ′与△OQC的外接圆⊙O′交于点S,连接CS,
∵∠OQC=∠OSC,∠OSC>∠OQ′C,
∴∠OQC>∠OQ′C,
∴当点Q在线段OC的垂直平分线上时,∠OQC最大.
过点O作OG⊥CQ于G,如图2②,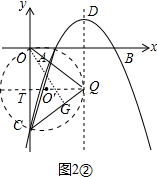
∵OT=TC=$\frac{1}{2}$OC=$\frac{3}{2}$,QT=2,
∴点Q的坐标为(2,-$\frac{3}{2}$),
OQ=CQ=$\sqrt{(\frac{3}{2})^{2}+{2}^{2}}$=$\frac{5}{2}$.
∵S△OQC=$\frac{1}{2}$OC•QT=$\frac{1}{2}$CQ•OG,
∴OG=$\frac{OC•QT}{CQ}$=$\frac{3×2}{\frac{5}{2}}$=$\frac{12}{5}$,
∴sin∠OQC=$\frac{OG}{OQ}$=$\frac{\frac{12}{5}}{\frac{5}{2}}$=$\frac{24}{25}$.
点评 本题主要考查了运用待定系数法求抛物线的解析式、抛物线上点的坐标特征、圆周角定理、三角函数、三角形外角的性质、解一元二次方程、勾股定理等知识,将∠DAP=∠ACB转化为∠PAB=∠OCA是解决第(2)小题的关键,构造辅助圆是解决第(3)小题的关键.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | x2+xy+1=x(x+y)+1 | B. | a2-b2=(a+b)(a-b) | ||
| C. | x2-4xy+4y2=(x-2y)2 | D. | ma+mb+mc=m(a+b+c) |
| A. | ?ABCD是中心对称图形 | B. | △AOB与△BOC的面积相等 | ||
| C. | △AOB≌△COD | D. | △AOB≌△BOC |
| A. | 0.25×10-7m | B. | 2.5×106m | C. | 2.5×10-6m | D. | 2.5×10-8m |
 如图,⊙P过平面直角坐标系原点O和x轴交于点A(8,0),和y轴交于点B(0,-6),⊙P的切线DC垂直于y轴,垂足为D,连接OC.
如图,⊙P过平面直角坐标系原点O和x轴交于点A(8,0),和y轴交于点B(0,-6),⊙P的切线DC垂直于y轴,垂足为D,连接OC.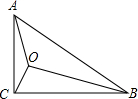 如图,在Rt△ABC中,∠C=90°,AC=2cm,BC=2$\sqrt{3}$cm,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°.按要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′).
如图,在Rt△ABC中,∠C=90°,AC=2cm,BC=2$\sqrt{3}$cm,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°.按要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′).