题目内容
20.?ABCD的对角线相交于点O,下列结论错误的是( )| A. | ?ABCD是中心对称图形 | B. | △AOB与△BOC的面积相等 | ||
| C. | △AOB≌△COD | D. | △AOB≌△BOC |
分析 由平行四边形的性质得出OA=OC,OB=OD,得出△AOB的面积=△BOC的面积,平行四边形是中心对称图形,由SAS证出△AOB≌△COD;即可得出结论.
解答 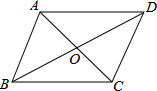 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴△AOB的面积=△BOC的面积,平行四边形是中心对称图形,
在△AOB和△COD中,
$\left\{\begin{array}{l}{OA=OC}\\{∠AOB=∠COD}\\{OB=OC}\end{array}\right.$,
∴△AOB≌△COD(SAS),
∴A、B、C正确,D错误;
故选:D.
点评 本题考查了平行四边形的性质、全等三角形的判定、三角形的面积;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
10.下列二次根式与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{45}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{6}$ |
11.在?ABCD中,如果添加一个条件,就可推出?ABCD是矩形,那么添加的条件可以是( )
| A. | AB=BC | B. | AC=BD | C. | AC⊥BD | D. | AB⊥BD |
12.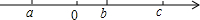 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
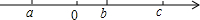 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )| A. | -a<b<c | B. | ab<ac | C. | -a+b>-a+c | D. | |a-b|<|a-c| |
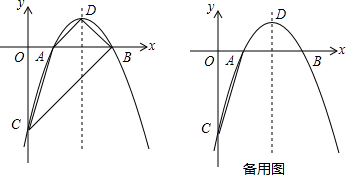
 如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°
如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°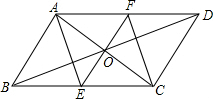 如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.
如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.