题目内容
19.如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2017的直角顶点的横坐标为( )
| A. | 8054 | B. | 8063 | C. | 8064 | D. | 8061 |
分析 先利用勾股定理计算出AB,从而得到△ABC的周长为12,根据旋转变换可得△OAB的旋转变换为每3次一个循环,由于2017÷3=672…1,于是可判断三角形2012与三角形1的状态一样,然后计算672×12即可得到三角形2017的直角顶点坐标.
解答 解:∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴△ABC的周长=3+4+5=12,
∵△OAB每连续3次后与原来的状态一样,
∵2017÷3=672…1,
∴△2017的直角顶点是第672个循环组后第一个三角形的直角顶点,
∴三角形2017的直角顶点的横坐标=672×12=8064,
∴三角形2017的直角顶点坐标为(8064,0),
故选C.
点评 此题考查了坐标与图形变化-旋转,仔细观察图形得到每三个三角形为一个循环组依次循环是解题的关键,也是求解的难点.

练习册系列答案
相关题目
9.多项式ab-bc+a2-c2分解因式的结果是( )
| A. | (a-c)(a+b+c) | B. | (a-c)(a+b-c) | C. | (a+c)(a+b-c) | D. | (a+c)(a-b+c) |
10.因式分解与整数乘法一样,都是一种恒等变形,即在变形的过程中,形变值不变,于是将多项式x2-y2+(2x+2y)分解因式的结果为( )
| A. | (x+y)(x-y+2) | B. | (x+y)(x-y-2) | C. | (x-y)(x-y+2) | D. | (x-y)(x-y-2) |
14.已知反比例函数y=$\frac{k}{x}$的图象经过点(2,3),那么下列各点在此函数图象上的是( )
| A. | (-6,1) | B. | (-1,-6) | C. | (2,-3) | D. | (3,-2) |
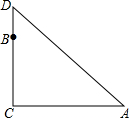 如图,在一棵树CD的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘的A处,另一只爬到树顶D后直接跃到A处,距离以直线计算.如果两只猴子所经过的距离相等,请问这棵树有多高?
如图,在一棵树CD的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘的A处,另一只爬到树顶D后直接跃到A处,距离以直线计算.如果两只猴子所经过的距离相等,请问这棵树有多高?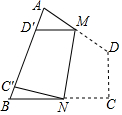 如图,四边形纸片ABCD中,∠A=75°,∠B=65°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=80°.
如图,四边形纸片ABCD中,∠A=75°,∠B=65°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=80°.