题目内容
10.因式分解与整数乘法一样,都是一种恒等变形,即在变形的过程中,形变值不变,于是将多项式x2-y2+(2x+2y)分解因式的结果为( )| A. | (x+y)(x-y+2) | B. | (x+y)(x-y-2) | C. | (x-y)(x-y+2) | D. | (x-y)(x-y-2) |
分析 先将前两项做一组利用平方差公式分解,再提取x+y即可得.
解答 解:x2-y2+(2x+2y)=(x+y)(x-y)+2(x+y)=(x+y)(x-y+2),
故选:A.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
15.若正比例函数的图象经过(-3,2),则这个图象一定经过点( )
| A. | (2,-3) | B. | $({\frac{3}{2},-1})$ | C. | (-1,1) | D. | (2,-2) |
19.如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2017的直角顶点的横坐标为( )


| A. | 8054 | B. | 8063 | C. | 8064 | D. | 8061 |
 如图,?ABCD的对角线AC、BD相交于点O,点E是BC的中点,若△ABD的周长为8cm,则△BOE的周长是4cm.
如图,?ABCD的对角线AC、BD相交于点O,点E是BC的中点,若△ABD的周长为8cm,则△BOE的周长是4cm.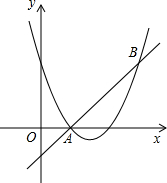 如图,直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
如图,直线y=x-1和抛物线y=x2+bx+c都经过点A(1,0),B(3,2). 如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C(0,4),顶点为(1,$\frac{9}{2}$).
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C(0,4),顶点为(1,$\frac{9}{2}$).