题目内容
20．
如图，在△ABC中，∠C=90°，AD是△ABC的角平分线，DE⊥AB于E，且DE=3cm，∠BAC=60°，则BC=9cm．
分析 根据三角形内角和定理求出∠B，根据角平分线性质求出DE，根据含30°角的直角三角形性质求出BD即可．
解答 解：△ABC中，∠C=90°，∠BAC=60°，
∴∠B=30°，
∵∠C=90°，AD是△ABC的角平分线，DE⊥AB，DE=3cm，
∴DE=DC=3cm，∠BED=90°，
∴BD=2DE=6cm，
∴BC=BD+CD=6cm+3cm=9cm，
故答案为：9．
点评 本题考查了三角形内角和定理，角平分线性质，含30°角的直角三角形性质的应用，能求出DE长和∠B的度数是解此题的关键．
练习册系列答案
相关题目
10．绝对值小于3.5的整数共有（ ）
| A． | 3个 | B． | 5个 | C． | 7个 | D． | 9个 |
8．某城市按以下规定收取每月煤气费：用煤气如果不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费．已知某用户4月份的煤气使用量为75立方米，那么4月份该用户应交煤气费（ ）
| A． | 60元 | B． | 90元 | C． | 75元 | D． | 66元 |
15．设A（1，y1），B（2，y2）是抛物线y=-（x+1）2+m上的两点，则y1，y2的大小关系为（ ）
| A． | y1≤y2 | B． | y1＜y2 | C． | y1≥y2 | D． | y1＞y2 |
已知：如图，在△ABC中，AB=AC，点D在AB上，且CB=CD=AD，求：△CBD各角的度数．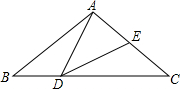
如图，在△ABC中，AB=AC=2，点D在线段BC上运动（点D不与B、C重合），∠B=40°，连结AD，作∠ADE=40°，DE交线段AC于E．
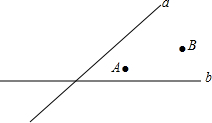李明准备与朋友经营一个超市，经调查发现他家附近有两个大的居民区A、B，同时又有相交的两条公路a、b（如图所示），李明想把超市建在到两居民区的距离，到两公路的距离分别相等的位置上，请用尺规作图确定超市P的位置．（作图不写作法，但要求保留作图痕迹）
10．九年级数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤70且x为整数）天的售价目与销量的相关信息如下表：
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于3250元？请直接写出结果．
| 时间x（天） | 1≤x≤40 | 40≤x≤70 |
| 售价（元/件） | x+45 | 85 |
| 每天销售（件） | 150-2x | |
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于3250元？请直接写出结果．