题目内容
7.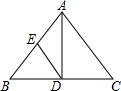 如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.
如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.
分析 由等腰三角形的三线合一性质得出AD⊥BC,BD=CD=$\frac{1}{2}$BC=9cm,由勾股定理求出AD,由直角三角形斜边上的中线性质得出DE=$\frac{1}{2}$AB=AE=7.5cm,即可得出△ADE的周长.
解答 解:∵AB=AC=15cm,AD是角平分线,
∴AD⊥BC,BD=CD=$\frac{1}{2}$BC=9cm,
∴∠ADB=90°,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12(cm),
∵E是AB的中点,
∴DE=$\frac{1}{2}$AB=AE=7.5cm,
∴△ADE的周长=AE+DE+AD=7.5+7.5+12=27(cm);
故答案为:27.
点评 本题考查了等腰三角形的性质、勾股定理、直角三角形斜边上的中线性质;熟练掌握等腰三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
17.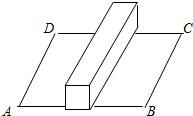 如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
 如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体的木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是30米.
18.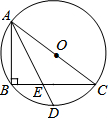 如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )
如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )
 如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )
如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )| A. | 3:4 | B. | 1:3 | C. | 2:3 | D. | 2:5 |
16.若x2+ax=(x+$\frac{1}{2}$)2+b,则a,b的值为( )
| A. | a=1,b=$\frac{1}{4}$ | B. | a=1,b=-$\frac{1}{4}$ | C. | a=0,b=-$\frac{1}{2}$ | D. | a=2,b=$\frac{1}{2}$ |
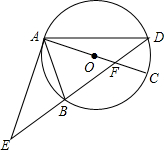 如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.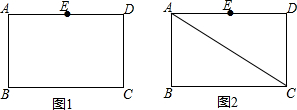
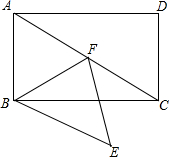 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.