题目内容
17.设直线y=-x+2k+7与直线y=x+4k-3的交点M不在第二象限,求k的取值范围.分析 设M(x,y),解方程组$\left\{\begin{array}{l}{y=-x+2k+7}\\{y=x+4k-3}\end{array}\right.$得M的交点坐标,求出如果M在第二象限,k>5,于是得到M不在第二象限,k的取值范围是k≤5.
解答 解:解$\left\{\begin{array}{l}{y=-x+2k+7}\\{y=x+4k-3}\end{array}\right.$得$\left\{\begin{array}{l}{x=-k+5}\\{y=3k+2}\end{array}\right.$,
∵点M是直线y=-x+2k+7与直线y=x+4k-3的交点,
∴M(-k+5,3k+2),
如果M在第二象限,则$\left\{\begin{array}{l}{x=-k+5<0}\\{y=3k+2>0}\end{array}\right.$,
解得k>5,
∵M不在第二象限,
∴k≤5,
∴k的取值范围是:k≤5.
点评 本题考查了两条直线相交或平行的问题,解方程组求函数的交点坐标,熟练掌握解方程组求函数的交点坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.我国四部地区约占我国国土面积的$\frac{2}{3}$,我国国土面积约960万平方公里.若用科学记数法表示,则我国四部地区的面积是( )
| A. | 6.4×107平方公里 | B. | 6.4×106平方公里 | C. | 64×105平方公里 | D. | 640×104平方公里 |
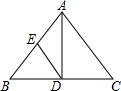 如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.
如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.
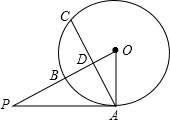 如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.
如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.