题目内容
19.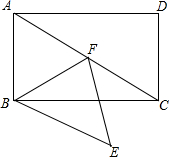 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,∠CBE=30°,求AC的长.
分析 (1)由外角的性质可得∠AFB=∠FBC+∠FCB,又因为∠ABF=∠FBC+∠FCB,易得AB=AF,由菱形的判定定理可得结论;
(2)作DH⊥AC于点H,由特殊角的三角函数可得∠CBE=30°,由平行线的性质可得∠2=∠CBE=30°,利用锐角三角函数可得AH,DH,由菱形的性质和勾股定理得CH,得AC.
解答 (1)证明:∵EF∥AB,BE∥AF,
∴四边形ABEF是平行四边形.
∵∠ABF=∠FBC+∠FCB,∠AFB=∠FBC+∠FCB,
∴∠ABF=∠AFB,
∴AB=AF,
∴?ABEF是菱形;
(2)解:作DH⊥AC于点H,
∵∠CBE=30°,
∵BE∥AC,
∴∠1=∠CBE,
∵AD∥BC,
∴∠2=∠1,
∴∠2=∠CBE=30°,
Rt△ADH中,AH=AD•cos∠2=4$\sqrt{3}$,
DH=AD•sin∠2=4,
∵四边形ABEF是菱形,
∴CD=AB=BE=5,
Rt△CDH中,CH=$\sqrt{C{D}^{2}-D{H}^{2}}$=3,
∴AC=AH+CH=4$\sqrt{3}$+3.
点评 本题主要考查了菱形的性质及判定定理,锐角三角函数等,由锐角三角函数解得AH,CH是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.抛物线y=x2-2x+1向左平移2个单位长度后,所得到的抛物线与x轴的交点坐标为( )
| A. | (-3,0) | B. | (-2,0) | C. | (-1,0) | D. | (3,0) |
11.有下列四种说法:
(1)过直线外一点有且只有一条直线与这条直线平行
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短
(4)平行于同一条直线的两条直线平行.
其中正确的个数是( )
(1)过直线外一点有且只有一条直线与这条直线平行
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短
(4)平行于同一条直线的两条直线平行.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.我国四部地区约占我国国土面积的$\frac{2}{3}$,我国国土面积约960万平方公里.若用科学记数法表示,则我国四部地区的面积是( )
| A. | 6.4×107平方公里 | B. | 6.4×106平方公里 | C. | 64×105平方公里 | D. | 640×104平方公里 |
 某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).
某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).
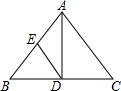 如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.
如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.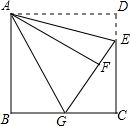 已知:如图,四边形ABCD为正方形,E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G.
已知:如图,四边形ABCD为正方形,E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G.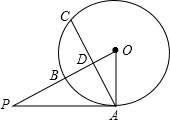 如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.
如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.