题目内容
18.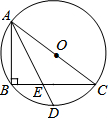 如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )
如图,Rt△ABC内接于⊙O,AB=3,BC=4,点D为$\widehat{BC}$的中点,连结AD与BC相交于点E,则DE:AE等于( )| A. | 3:4 | B. | 1:3 | C. | 2:3 | D. | 2:5 |
分析 根据垂径定理得到OD⊥BC,CM=$\frac{1}{2}$BC=2,推出△ABE∽△DME,得到比例式,代入数值即可得到结果.
解答  解:连接OD交BC于M,
解:连接OD交BC于M,
∵点D为$\widehat{BC}$的中点,
∴OD⊥BC,CM=$\frac{1}{2}$BC=2,
∴∠DME=∠B=90°,
∵∠AEB=∠DEM,
∴△ABE∽△DME,
∴$\frac{AE}{DE}=\frac{AB}{DM}$,
∵Rt△ABC内接于⊙O,
∴AC是⊙O的直径.
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∴OC=OD=$\frac{5}{2}$,
∴(OD-DM)2+CM2=OC2,
即($\frac{5}{2}$-DM)2+22=($\frac{5}{2}$)2,
∴DM=1,DM=4(不合题意舍去),
∴DE:AE=DM:AB=1:3.
故选B.
点评 本题考查了相似三角形的判定和性质,圆周角定理,垂径定理,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8.下列计算正确的是( )
| A. | (a-b)2=a2-b2 | B. | -(a-1)=-a-1 | C. | a3+a2=2a5 | D. | (-2a3)2=4a6 |
13.满足不等式2x<-1最大整数解的x值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
8.我国四部地区约占我国国土面积的$\frac{2}{3}$,我国国土面积约960万平方公里.若用科学记数法表示,则我国四部地区的面积是( )
| A. | 6.4×107平方公里 | B. | 6.4×106平方公里 | C. | 64×105平方公里 | D. | 640×104平方公里 |
 某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).
某校数学课外实践活动小组想利用所学知识测量南明湖的宽度.如图所示是南明湖的一段,两岸AB∥CD,河对岸E处有一座房子,小组成员用测角仪在F处测得∠EFD=36°,往前走205米后到达点G处,测得∠EGD=72°,请你根据这些数据帮该小组算出湖宽EH(结果精确到0.1).
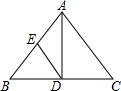 如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.
如图,在等腰△ABC中,AD是角平分线,E是AB的中点,已知AB=AC=15cm.BC=18cm,则△ADE的周长是27cm.