题目内容
14.求x和y的值:(1)$\sqrt{{x}^{2}-16}$+$\sqrt{13-y}$=0;
(2)(x-2y)2+$\sqrt{2x-3y-1}$=0.
分析 (1)首先根据任何数的算术平方根是非负数,两个非负数的和是0,则每个非负数等于0,据此即可求的x和y的值;
(2)首先根据任何数的平方、绝对值都是非负数,两个非负数的和是0,则每个非负数等于0,据此即可求的x和y的值.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{{x}^{2}-16=0}\\{13-y=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=13}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=13}\end{array}\right.$;
(2)根据题意得:$\left\{\begin{array}{l}{x-2y=0}\\{2x-3y-1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 本题考查了非负数的性质,两个非负数的和是0,则每个非负数等于0,初中范围内的非负数有:任何数的偶次方、算术平方根以及绝对值.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
4.已知点A(-3,m)与点B(2,n)是直线y=-$\frac{2}{3}$x+b上的两点,则m与n的大小关系是( )
| A. | m>n | B. | m=n | C. | m<n | D. | 无法确定 |
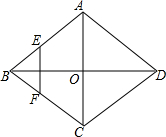 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.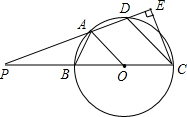 已知四边形ABCD内接于以BC为直径的⊙O,A为弧BD中点,延长CB,DA交于点P.
已知四边形ABCD内接于以BC为直径的⊙O,A为弧BD中点,延长CB,DA交于点P.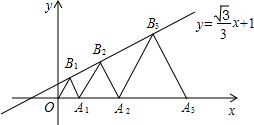 如图,点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线y=$\frac{\sqrt{3}}{3}$x+1上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形.则A2016的横坐标为22016$\sqrt{3}$-$\sqrt{3}$.
如图,点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线y=$\frac{\sqrt{3}}{3}$x+1上,△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形.则A2016的横坐标为22016$\sqrt{3}$-$\sqrt{3}$.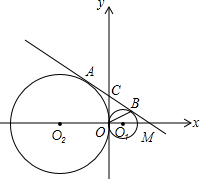 如图,⊙O1与⊙O2外切于点O,直线AB分别与⊙O1、⊙O2切于点B、A,分别与x轴、y轴交于点M(2$\sqrt{3}$,0)、C(0,2).
如图,⊙O1与⊙O2外切于点O,直线AB分别与⊙O1、⊙O2切于点B、A,分别与x轴、y轴交于点M(2$\sqrt{3}$,0)、C(0,2).