题目内容
17.已知整式p=x2+x-1,Q=x2-x+1.R=-x2+x+1,若一个次数不高于二次的整式可以表示为aP+bQ+cR(其中a、b、c为常数).则可以进行如下分类:①若a≠0,b=c=0,则称该整式为P类整式;
②若a≠0,b≠0,c=0,则称该整式为PQ类整式;
③若a≠0,b≠0,c≠0.则称该整式为PQR类整式.
…
(1)模仿上面的分类方式,请给出R类整式和QR类整式的定义.
若a=b=0,c≠0,则称该整式为“R类整式”.
若a=0,b≠0,c≠0,则称该整式为“QR类整式”.
(2)例如x2-5x+5则称该整式为“PQ类整式”,因为-2P+3Q=-2(x2+x-1)+3(x2-x-1)
=-2x2-2x+2+3x2-3x+3=x2-5x+5.
即x2-5x+5=-2P+3Q,所以x2-5x+5是“PQ类整式”
问题:x2+x+1是哪一类整式?请通过列式计算说明.
(3)试说明4x2+11x+2015是“PQR类整式”,并求出相应的a,b,c的值.
分析 (1)类比的出R类整式和QR类整式的定义即可;
(2)类比方法拆开表示得出答案即可;
(3)利用给出的PQR类整式得意义待定得出a、b、c的数值即可.
解答 解:(1)若a=b=0,c≠0,则称该整式为“R类整式”.
若a=0,b≠0,c≠0,则称该整式为“QR类整式”.
(2)∵x2+x+1=(x2+x-1)+(x2-x+1)+(-x2+x+1),
∴该整式为PQR类整式.
(3)∵4x2+11x+2015是“PQR类整式”,
∴设4x2+11x+2015=a(x2+x-1)+b(x2-x+1)+c(-x2+x+1),
∴a+b-c=4,a-b+c=11,-a+b+c=2015,
解得:a=7.5,b=1009.5,c=1013.
点评 此题考查整式,理解题意,掌握给出的整式的特征,利用类比的方法得出答案即可.

练习册系列答案
相关题目
6.若|X|=3,|Y|=4,且X<Y,那么X+Y=( )
| A. | +1或+7 | B. | -1或-7 | C. | +1或-7 | D. | -1或+7 |
 如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.
如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.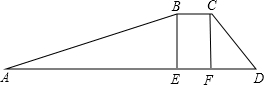 如图所示,拦水坝的横断面为梯形ABCD,斜坡AB的坡度为$\frac{1}{2.5}$,坝顶宽BC=2.8,坝高BE=4.2米,斜坡CD=7.5米.
如图所示,拦水坝的横断面为梯形ABCD,斜坡AB的坡度为$\frac{1}{2.5}$,坝顶宽BC=2.8,坝高BE=4.2米,斜坡CD=7.5米.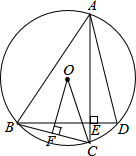 如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,
如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,