题目内容
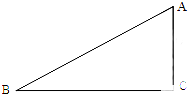 如图,在Rt△ABC中,∠C=90°,sinA=
如图,在Rt△ABC中,∠C=90°,sinA=| 3 |
| 4 |
(1)求AC的长;
(2)求cotB的值.
考点:解直角三角形
专题:
分析:(1)根据sinA的值求出AB,根据勾股定理求出AC即可;
(2)把BC和AC的值代入cotB=
求出即可.
(2)把BC和AC的值代入cotB=
| BC |
| AC |
解答:
解:(1)∵在Rt△ACB中,∠C=90°,sinA=
=
,BC=6,
∴AB=8,
由勾股定理得:AC=
=
=2
;
(2)cotB=
=
=
.
| 3 |
| 4 |
| BC |
| AB |
∴AB=8,
由勾股定理得:AC=
| AB2-BC2 |
| 82-62 |
| 7 |
(2)cotB=
| BC |
| AC |
| 6 | ||
2
|
3
| ||
| 7 |
点评:本题考查了勾股定理和解直角三角形的应用,能根据锐角三角函数的定义正确解直角三角形是解此题的关键,难度适中.

练习册系列答案
相关题目
已知等腰△ABC中,AD⊥BC于点D,且AD=
BC,则△ABC底角的度数为( )
| 1 |
| 2 |
| A、45°或75° |
| B、75° |
| C、45°或75°或15° |
| D、60° |
下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等.
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等.
| A、①②③ | B、③④⑤ |
| C、①②⑤ | D、②④⑤ |
如图,不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线.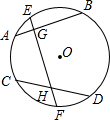 已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
 如图,BD,CD分别平分△ABC的两个外角,若∠A=α,求∠BDC的度数.
如图,BD,CD分别平分△ABC的两个外角,若∠A=α,求∠BDC的度数.