题目内容
已知等腰△ABC中,AD⊥BC于点D,且AD=
BC,则△ABC底角的度数为( )
| 1 |
| 2 |
| A、45°或75° |
| B、75° |
| C、45°或75°或15° |
| D、60° |
考点:含30度角的直角三角形,等腰三角形的性质
专题:分类讨论
分析:分三种情况讨论,先根据题意分别画出图形,当AB=AC时,根据已知条件得出AD=BD=CD,从而得出△ABC底角的度数;当AB=BC时,先求出∠ABD的度数,再根据AB=BC,求出底角的度数;当AB=BC时,根据AD=
BC,AB=BC,得出∠DBA=30°,从而得出底角的度数.
| 1 |
| 2 |
解答:
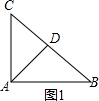 解:①如图1,当AB=AC时,
解:①如图1,当AB=AC时,
∵AD⊥BC,
∴BD=CD,
∵AD=
BC,
∴AD=BD=CD,
∴底角为45°;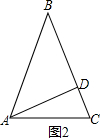
②如图2,当AB=BC时,
∵AD=
BC,
∴AD=
AB,
∴∠ABD=30°,
∴∠BAC=∠BCA=75°,
∴底角为75°.
③如图3,当AB=BC时,
∵AD=
BC,AB=BC,
∴AD=
AB,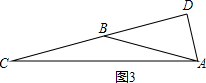
∴∠DBA=30°,
∴∠BAC=∠BCA=15°;
∴△ABC底角的度数为45°或75°或15°;
故选C.
 解:①如图1,当AB=AC时,
解:①如图1,当AB=AC时,∵AD⊥BC,
∴BD=CD,
∵AD=
| 1 |
| 2 |
∴AD=BD=CD,
∴底角为45°;

②如图2,当AB=BC时,
∵AD=
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |
∴∠ABD=30°,
∴∠BAC=∠BCA=75°,
∴底角为75°.
③如图3,当AB=BC时,
∵AD=
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |

∴∠DBA=30°,
∴∠BAC=∠BCA=15°;
∴△ABC底角的度数为45°或75°或15°;
故选C.
点评:此题考查了含30度角的直角三角形和等腰三角形的性质,关键是根据题意画出图形,注意不要漏解.

练习册系列答案
相关题目
若一个物体向东运动5米记作-5米,则+3表示该物体( )
| A、向东运动3米 |
| B、向南运动3米 |
| C、向西运动3米 |
| D、向北运动3米 |
 如图,是一个几何体的三视图,则这个几何体的形状是( )
如图,是一个几何体的三视图,则这个几何体的形状是( )| A、圆柱 | B、圆锥 | C、圆台 | D、长方体 |
向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0),若此炮弹在第6钞与第14秒时的高度相等,则炮弹达到最大高度的时间是( )
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
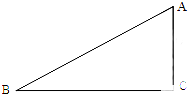 如图,在Rt△ABC中,∠C=90°,sinA=
如图,在Rt△ABC中,∠C=90°,sinA= 如图所示,已知AB∥CD,点E在直线AB上,射线EF交CD于点P,且∠FEB=50°,M为直线AB上一动点,射线MN过点P.
如图所示,已知AB∥CD,点E在直线AB上,射线EF交CD于点P,且∠FEB=50°,M为直线AB上一动点,射线MN过点P.