题目内容
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线.(1)求DE的长;
(2)连AE,求AE的长;
(3)若CE交AB于点F,求CF的长.
考点:线段垂直平分线的性质
专题:
分析:(1)如图,首先求出MF、CM、DF的长度;证明△CMF∽△EDF,得到
=
,求出DE即可解决问题.
(2)直接运用勾股定理求出AE即可解决问题.
(3)直接运用勾股定理求出CF即可解决问题.
| CM |
| DE |
| MF |
| DF |
(2)直接运用勾股定理求出AE即可解决问题.
(3)直接运用勾股定理求出CF即可解决问题.
解答:
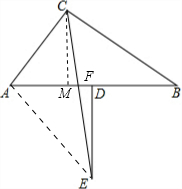 解:(1)如图,过点C作CM⊥AB于点M;
解:(1)如图,过点C作CM⊥AB于点M;
∵∠ACB=90°,AC=3,BC=4,
∴AB=
=5;而CF平分∠ACB,
∴
=
=
,而AF+BF=5,
解得:AF=
;由射影定理得:
AC2=AM•AB,
∴AM=
,MF=AF-AM=
,BM=5-AM=
;
由射影定理得:CM2=AM•BM,
∴CM=
;而DE是AB的中垂线,
∴AD=
AB=
,DF=
-
=
;
∵CM⊥AB,DE⊥AB,
∴△CMF∽△EDF,
∴
=
,而CM=
,MF=
,DF=
,
解得:DE=
.
(2)如图,由勾股定理得:AE2=AD2+DE2,
解得:AE=
.
(3)如图,由勾股定理得:
CF2=CM2+MF2,解得:CF=
.
 解:(1)如图,过点C作CM⊥AB于点M;
解:(1)如图,过点C作CM⊥AB于点M;∵∠ACB=90°,AC=3,BC=4,
∴AB=
| 32+42 |
∴
| AF |
| BF |
| AC |
| BC |
| 3 |
| 4 |
解得:AF=
| 15 |
| 7 |
AC2=AM•AB,
∴AM=
| 9 |
| 5 |
| 12 |
| 35 |
| 16 |
| 5 |
由射影定理得:CM2=AM•BM,
∴CM=
| 12 |
| 5 |
∴AD=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 15 |
| 7 |
| 5 |
| 14 |
∵CM⊥AB,DE⊥AB,
∴△CMF∽△EDF,
∴
| CM |
| DE |
| MF |
| DF |
| 12 |
| 5 |
| 12 |
| 35 |
| 5 |
| 14 |
解得:DE=
| 5 |
| 2 |
(2)如图,由勾股定理得:AE2=AD2+DE2,
解得:AE=
5
| ||
| 2 |
(3)如图,由勾股定理得:
CF2=CM2+MF2,解得:CF=
12
| ||
| 7 |
点评:该题主要考查了线段垂直平分线的性质、角平分线的性质、相似三角形的判定、勾股定理等几何知识点及其应用问题;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
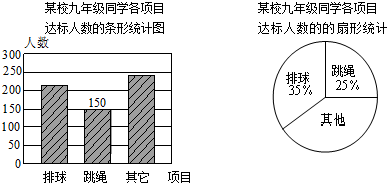
 一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )
一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
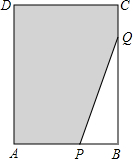 如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2.
如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2.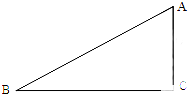 如图,在Rt△ABC中,∠C=90°,sinA=
如图,在Rt△ABC中,∠C=90°,sinA=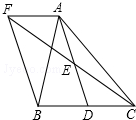 如图,在△ABC中,D是BC边上一点,E是AD的中点,过A作BC的平行线交CE的延长线F,且AF=BD,连结BF.
如图,在△ABC中,D是BC边上一点,E是AD的中点,过A作BC的平行线交CE的延长线F,且AF=BD,连结BF.