题目内容
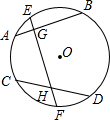已知：如图，G、H分别是⊙O的弦AB，CD的中点，OG=OH，求证： |
| AB |
|
| CD |
考点：圆心角、弧、弦的关系
专题：证明题
分析：可以根据圆的旋转不变性证明；也可以构造到全等三角形中证明．
解答：
证明：G，H分别为弦AB，CD的中点，
由圆的对称性可知OG⊥AB，OH⊥CD．
又∵OG=OH，
∴
=
．
由圆的对称性可知OG⊥AB，OH⊥CD．
又∵OG=OH，
∴
|
| AB |
|
| CD |
点评：本题所证明的结论：在同圆或等圆中，等弦的弦心距相等，圆心角相等，所对的弧也相等．
练习册系列答案
相关题目
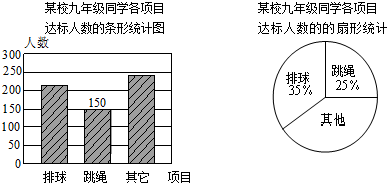
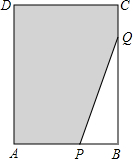如图，在长方形ABCD中，AB=6，CB=8，点P与点Q分别是AB，CB边上的动点，点P与点Q同时出发，点P以每秒2个单位长度的速度从点A→点B运动，点Q以每秒1个单位长度的速度从点C→点B运动．当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t秒，阴影部分的面积为Sm2．
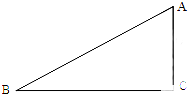如图，在Rt△ABC中，∠C=90°，sinA=向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y=ax2+bx+c（a≠0），若此炮弹在第6钞与第14秒时的高度相等，则炮弹达到最大高度的时间是（ ）
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
如图，由24个边长为1的正方形组成4×6的网格．若△A′B′C′∽△ABC（相似比不是1），且△A′B′C′，△ABC的顶点都是网格内正方形的顶点，则△A′B′C′的面积是