题目内容
19.解方程组:$\frac{x-2y+z}{9}$=$\frac{2x+y+3z}{10}$=$\frac{3x+2y-4z}{3}$=1.分析 先转化成方程组,①+③得出4x-3z=12④,①+②×2得出5x+7z=29⑤,由④和⑤组成一个二元一次方程组,求出x、z的值,把x、z的值代入①求出x即可.
解答 解:∵$\frac{x-2y+z}{9}$=$\frac{2x+y+3z}{10}$=$\frac{3x+2y-4z}{3}$=1,
∴$\left\{\begin{array}{l}{x-2y+z=9①}\\{2x+y+3z=10②}\\{3x+2y-4z=3③}\end{array}\right.$
①+③得:4x-3z=12④,
①+②×2得:5x+7z=29⑤,
由④和⑤组成一个二元一次方程组$\left\{\begin{array}{l}{4x-3z=12}\\{5x+7z=29}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=\frac{171}{43}}\\{z=\frac{56}{43}}\end{array}\right.$,
把x、z的值代入①得:$\frac{171}{43}$-2y+$\frac{56}{43}$=9,
解得:y=-$\frac{107}{43}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{171}{43}}\\{y=-\frac{107}{43}}\\{z=\frac{56}{43}}\end{array}\right.$.
点评 本题考查了解三元一次方程组的应用,解此题的关键是能把三元一次方程组转化成二元一次方程组,难度适中.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
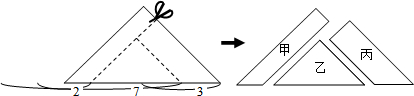

| A. | 乙>丙>甲 | B. | 丙>乙>甲 | C. | 甲>丙>乙 | D. | 无法判断 |
 如图,两直线l1,l2的交点坐标(2,2)可以作是某个关于x,y的方程组的解,求这个方程组.
如图,两直线l1,l2的交点坐标(2,2)可以作是某个关于x,y的方程组的解,求这个方程组.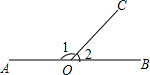 如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,设∠1,∠2的度数分别为x,y,那么可以列出的方程组是$\left\{\begin{array}{l}{x+y=180}\\{x=3y-10}\end{array}\right.$.
如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,设∠1,∠2的度数分别为x,y,那么可以列出的方程组是$\left\{\begin{array}{l}{x+y=180}\\{x=3y-10}\end{array}\right.$. 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(2,2)与点B(4,m),则△AOB的面积为3.
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(2,2)与点B(4,m),则△AOB的面积为3.