题目内容
9.计算(1)解方程组$\left\{\begin{array}{l}{2x-y=1}\\{3x-\frac{y+1}{2}=4}\end{array}\right.$
(2)计算:(1-$\sqrt{2}$)0-$\sqrt{3}$tan30°+($\frac{1}{3}$)-2.
分析 (1)首先化简可得$\left\{\begin{array}{l}{2x-y=1①}\\{6x-y=9②}\end{array}\right.$,然后利用减法消未知数y,可得x的值,然后可得y的值;
(2)本题涉及零指数幂、负整数指数幂、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)组$\left\{\begin{array}{l}{2x-y=1}\\{3x-\frac{y+1}{2}=4}\end{array}\right.$,
化简得:$\left\{\begin{array}{l}{2x-y=1①}\\{6x-y=9②}\end{array}\right.$,
②-①得:4x=8,
解得:x=2,
把x=2代入①得:y=3,
所以方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
(2)(1-$\sqrt{2}$)0-$\sqrt{3}$tan30°+($\frac{1}{3}$)-2
=1-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$+9
=1-1+9
=9.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.

练习册系列答案
相关题目
15.某超市一月份的营业额为36万元,三月份的营业额为48万元.设每月的平均增长率为x,则可列方程为( )
| A. | 48(1+x)2=36 | B. | 48(1-x)2=36 | C. | 36(1-x)2=48 | D. | 36(1+x)2=48 |
1. 已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
 已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )| A. | 3cm | B. | 6cm | C. | 12cm | D. | 无法确定 |

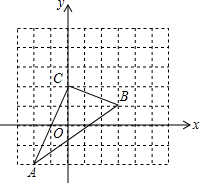 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,