题目内容
9.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )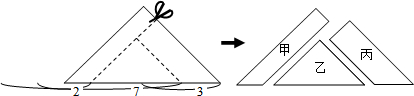
| A. | 乙>丙>甲 | B. | 丙>乙>甲 | C. | 甲>丙>乙 | D. | 无法判断 |
分析 首先过点B作BH⊥GF于点H,则S乙=$\frac{1}{2}$AB•AC,易证得△ABC∽△DBE,△GBH∽△BCA,可求得GF,DB,DE,DF的长,继而求得答案.
解答 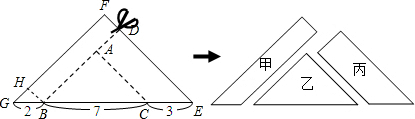 解:如图:过点B作BH⊥GF于点H,
解:如图:过点B作BH⊥GF于点H,
则S乙=$\frac{1}{2}$AB•AC,
∵AC∥DE,
∴△ABC∽△DBE,
∴$\frac{AC}{DE}$=$\frac{AB}{DB}$=$\frac{BC}{BE}$,
∵BC=7,CE=3,
∴DE=$\frac{10}{7}$AC,DB=$\frac{10}{7}$AB,
∴AD=BD-BA=$\frac{3}{7}$AB,
∴S丙=$\frac{1}{2}$(AC+DE)•AD=$\frac{51}{98}$AB•AC,
∵AD∥GF,BH⊥GF,AC⊥AB,
∴BH∥AC,
∴四边形BDFH是矩形,
∴BH=DF,FH=BD=$\frac{10}{7}$AB,
∴△GBH∽△BCA,
∴$\frac{GH}{AB}$=$\frac{BH}{AC}$=$\frac{GB}{BC}$,
∵GB=2,BC=7,
∴GH=$\frac{2}{7}$AB,BH$\frac{2}{7}$AC,
∴DF=$\frac{2}{7}$AC,GF=GH+FH=$\frac{12}{7}$AB,
∴S甲=$\frac{1}{2}$(BD+GF)•DF=$\frac{22}{49}$AB•AC,
∴甲<乙<丙.
故选:B.
点评 此题考查了相似三角形的判定与性质、直角梯形的性质以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
20.下列说法正确的是( )
| A. | 在促销活动中某商品的中奖率是万分之一,则购买该商品一万件就一定会中奖 | |
| B. | 为了解某品牌节能灯的使用寿命,采用了普查的方式 | |
| C. | 一组数据6,7,8,8,9,10的众数和平均数都是8 | |
| D. | 若甲组数据的方差S甲2=0.05,乙组数据的方差S乙2=0.1,则乙组数据比甲组数据稳定 |
1.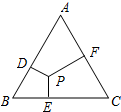 如图,P为边长为2的正三角形内任意一点,过P点分别作三边的垂线,垂足分别为D,E,F,则PD+PE+PF的值为( )
如图,P为边长为2的正三角形内任意一点,过P点分别作三边的垂线,垂足分别为D,E,F,则PD+PE+PF的值为( )
 如图,P为边长为2的正三角形内任意一点,过P点分别作三边的垂线,垂足分别为D,E,F,则PD+PE+PF的值为( )
如图,P为边长为2的正三角形内任意一点,过P点分别作三边的垂线,垂足分别为D,E,F,则PD+PE+PF的值为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
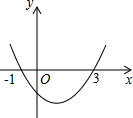 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0)和(3,0).对于下列结论:①abc>0;②b-2a=0;③a-b+c<0;④a+b+c>0;⑤b2-4ac>0.其中结论正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0)和(3,0).对于下列结论:①abc>0;②b-2a=0;③a-b+c<0;④a+b+c>0;⑤b2-4ac>0.其中结论正确的是( )