题目内容
10. 如图,两直线l1,l2的交点坐标(2,2)可以作是某个关于x,y的方程组的解,求这个方程组.
如图,两直线l1,l2的交点坐标(2,2)可以作是某个关于x,y的方程组的解,求这个方程组.
分析 因为函数图象交点坐标为两函数解析式组成的方程组的解.因此本题应该先用待定系数法求出两条直线的解析式,联立两直线解析式所组成的方程组即为所求的方程组.
解答 解:由图知:两函数的图象经过点(2,2),(3,0),(0,3),
可求得两直线的解析式为:y=-2x+6和y=-$\frac{1}{2}$x+3,
因而直线l1,l2的交点坐标可以看作方程组$\left\{\begin{array}{l}{y=-2x+6}\\{y=-\frac{1}{2}x+3}\end{array}\right.$即$\left\{\begin{array}{l}{2x+y=6}\\{\frac{1}{2}x+y=3}\end{array}\right.$的解.
点评 此题考查一次函数和方程组问题,在同一平面直角坐标系中,两个一次函数图象的交点坐标就是相应的二元一次方程组的解.反过来,以二元一次方程组的解为坐标的点,一定是相应的两个一次函数的图象的交点.

练习册系列答案
相关题目
1. 已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
 已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )| A. | 3cm | B. | 6cm | C. | 12cm | D. | 无法确定 |
20.下列说法正确的是( )
| A. | 在促销活动中某商品的中奖率是万分之一,则购买该商品一万件就一定会中奖 | |
| B. | 为了解某品牌节能灯的使用寿命,采用了普查的方式 | |
| C. | 一组数据6,7,8,8,9,10的众数和平均数都是8 | |
| D. | 若甲组数据的方差S甲2=0.05,乙组数据的方差S乙2=0.1,则乙组数据比甲组数据稳定 |
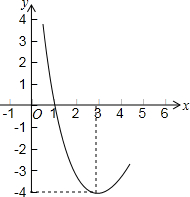 如图是二次函数的部分图象.
如图是二次函数的部分图象.