题目内容
 如图所示,在⊙O中,
如图所示,在⊙O中, |
| AD |
 |
| AC |
(1)求∠B的度数;
(2)圆心O到弦AC的距离;
(3)求图中阴影部分面积.
考点:圆周角定理,垂径定理,扇形面积的计算
专题:
分析:(1)根据圆周角定理得出∠B=∠ACD,即可得出答案;
(2)过O作OH⊥AC于H,连接OA、OC,根据圆周角定理求出∠AOC,求出∠AOH,解直角三角形求出即可;
(3)分别求出扇形AOC的面积和△AOC的面积,即可得出答案.
(2)过O作OH⊥AC于H,连接OA、OC,根据圆周角定理求出∠AOC,求出∠AOH,解直角三角形求出即可;
(3)分别求出扇形AOC的面积和△AOC的面积,即可得出答案.
解答:解:(1)∵
=
,
∴∠B=∠ACD=60°;
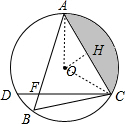 (2)过O作OH⊥AC于H,连接OA、OC,
(2)过O作OH⊥AC于H,连接OA、OC,
∵根据圆周角定理得:∠AOC=2∠B=120°,
∴∠AOH=
∠AOC=60°,
∴OH=OA•cos∠AOH=2×
=1,
即圆心O到AC的距离为1cm;
(3)∵AH=AO•sin∠AOH=2×
=
,
∴AC=2AH=2
,
S阴影=S扇形OAC-S△AOC
=
×π×22-
×2
×1
=(
π-
)cm2.
 |
| AD |
 |
| AC |
∴∠B=∠ACD=60°;
 (2)过O作OH⊥AC于H,连接OA、OC,
(2)过O作OH⊥AC于H,连接OA、OC,∵根据圆周角定理得:∠AOC=2∠B=120°,
∴∠AOH=
| 1 |
| 2 |
∴OH=OA•cos∠AOH=2×
| 1 |
| 2 |
即圆心O到AC的距离为1cm;
(3)∵AH=AO•sin∠AOH=2×
| ||
| 2 |
| 3 |
∴AC=2AH=2
| 3 |
S阴影=S扇形OAC-S△AOC
=
| 120 |
| 360 |
| 1 |
| 2 |
| 3 |
=(
| 4 |
| 3 |
| 3 |
点评:本题考查了圆周角定理,解直角三角形,垂径定理的应用,能综合性运用定理进行推理和计算是解此题的关键,难度适中.

练习册系列答案
相关题目
小明由等积式5x=6y写了以下比例式:①
=
;②
=
;③
=
;④
=
,则小明写出的比例式中正确的是( )
| y |
| x |
| 5 |
| 6 |
| x |
| y |
| 5 |
| 6 |
| x |
| 6 |
| y |
| 5 |
| 5 |
| x |
| y |
| 6 |
| A、①③ | B、②③ | C、②④ | D、③④ |
 如图,在菱形ABCD中,对角线AC与BD相交于点O,点E是边AB的中点,CD=4,则OE的长是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,点E是边AB的中点,CD=4,则OE的长是( )| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
在同一平面内,连接一个定点和圆上的任意一点的线段中,最短为4cm,最长为9cm,则该圆的半径是( )
| A、2.5cm或6.5cm |
| B、2.5cm |
| C、6.5cm |
| D、5cm或13cm |
已知k1<0<k2,则函数y=k1x和y=
的图象大致是( )
| k2 |
| x |
A、 |
B、 |
C、 |
D、 |
 若正三角形的边长为2
若正三角形的边长为2 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: 长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.
长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°. 如图,一只船由原点O出发,航行40海里至A点,接着又航行12海里至B点,已知∠1=60°,∠2=45°,求B点的坐标.
如图,一只船由原点O出发,航行40海里至A点,接着又航行12海里至B点,已知∠1=60°,∠2=45°,求B点的坐标.