题目内容
10. 如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )
如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )| A. | 45° | B. | 30° | C. | 20° | D. | 22.5° |
分析 根据等边对等角的性质可得∠E=∠CAE,然后根据正方形的对角线平分一组对角以及三角形的一个外角等于与它不相邻的两个内角的和列式求出∠E=∠CAE=22.5°,再由∠DAC=45°即可得解.
解答 解:∵CE=AC,
∴∠E=∠CAE,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,∠DAC=45°,
∴∠E+∠CAE=45°,
∴∠E=∠CAE=$\frac{1}{2}$×45°=22.5°,
∴∠DAF=∠DAC-∠CAE=45°-22.5°=22.5°,
故选D.
点评 本题考查了正方形的性质,等腰三角形的性质,主要利用了正方形的对角线平分一组对角,等边对等角,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.下列各式从左到右的变形是因式分解的是( )
| A. | (x-y)(x+y)=x2-y2 | B. | a2-4a+4=a(a-4)+4 | ||
| C. | m2n-8n=n(m+4)(m-4) | D. | 3(a-b)+a(b-a)=(a-b)(3-a) |
2.下列成语所描述的事件是必然事件的是( )
| A. | 拔苗助长 | B. | 瓮中捉鳖 | C. | 水中捞月 | D. | 守株待兔 |
19.与单项式2x2y是同类项的是( )
| A. | -2y | B. | x2 | C. | 3x2y2 | D. | -x2y |
20. 如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )
如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )
 如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )
如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )| A. | 155° | B. | 35° | C. | 135° | D. | 145° |
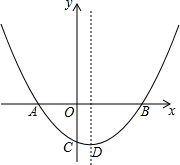 如图,抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
如图,抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.