题目内容
20. 如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )
如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )| A. | 155° | B. | 35° | C. | 135° | D. | 145° |
分析 先根据对顶角相等的性质得出∠1=∠2=35°,再把∠1=35°代入∠1=180°-α,即可求出α的度数.
解答 解:∵∠1与∠2是对顶角,∠2=35°,
∴∠1=∠2=35°,
∵∠1=180°-α,
∴35°=180°-α,
∴α=145°.
故选D.
点评 本题考查了对顶角相等的性质以及角度的计算,求出∠1=35°是解题的关键.

练习册系列答案
相关题目
10. 如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )
如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )
 如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )
如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )| A. | 45° | B. | 30° | C. | 20° | D. | 22.5° |
11.下列四组线段中,可以构成直角三角形的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 1.5,2,2.5 | D. | 1,$\sqrt{2}$,3 |
15.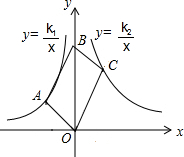 如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
 如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )| A. | -2k1 | B. | 2k2 | C. | k1+k2 | D. | k2-k1 |
12.下列数2,π,$\frac{22}{7}$,-$\sqrt{2}$,$\sqrt{9}$中,无理数的个数有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.已知y是x的一次函数,解析式为y=(k-1)x+k,它的图象不经过第三象限,那么k的范围是( )
| A. | k≥0 | B. | k≤1 | C. | 0≤k<1 | D. | 0<k≤1 |
17.一家公司打算招聘一名公关人员,对甲、乙、丙三名应试者进行了笔试、面试、实际操作三方面的测试,他们的各项成绩(百分制)如表:
(1)如果这家公司将笔试、面试、实际操作三项成绩按2:3:5的比例确定应试者的平均成绩,从他们的成绩看,应该录取谁?
(2)这家公司将笔试、面试、实际操作三项成绩按照一定比例确定应试者的平均成绩,已知实际操作占50%,面试成绩所占百分比为x(x>0),从成绩看,如果甲要想被录取,求x的取值范围应为多少?
| 应试者 | 笔试 | 面试 | 实际操作 |
| 甲 | 95 | 85 | 90 |
| 乙 | 90 | 95 | 85 |
| 丙 | 85 | 90 | 94 |
(2)这家公司将笔试、面试、实际操作三项成绩按照一定比例确定应试者的平均成绩,已知实际操作占50%,面试成绩所占百分比为x(x>0),从成绩看,如果甲要想被录取,求x的取值范围应为多少?
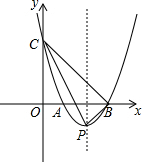 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0). 如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).
如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).