题目内容
4.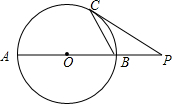 如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.
如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.
分析 由切线的性质可知∠PCO=90°,再根据斜边中线定理即可解决问题.
解答 解:如图,连接 OC.
OC.
∵PC切⊙O于C,
∴OC⊥PC,
∴∠PCO=90°,
∵OB=PB,OB=2$\sqrt{3}$,
∴BC=BO=PB=2$\sqrt{3}$,
故答案为2$\sqrt{3}$.
点评 本题考查切线的性质、直角三角形斜边中线定理,解题的关键是掌握切线的性质,知道切线垂直于过切点的半径,直角三角形斜边中线等于斜边一半,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.整式:-0.34x2y,π,$\frac{a+1}{2}$,-52xyz2,$\frac{1}{3}$x2-$\frac{1}{5}$y,-$\frac{1}{3}$xy2-$\frac{1}{2}$中,单项式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.已知一个正多边形的每个外角都等于72°,则这个正多边形是( )
| A. | 正五边形 | B. | 正六边形 | C. | 正七边形 | D. | 正八边形 |
9.下列运算中,计算正确的是( )
| A. | a3•a6=a9 | B. | (a2)3=a5 | C. | 4a3-2a2=2 | D. | (3a)2=6a2 |
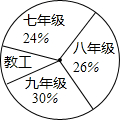 某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40.
某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40.