题目内容
13.如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为15°,45°,105°,135°,150°.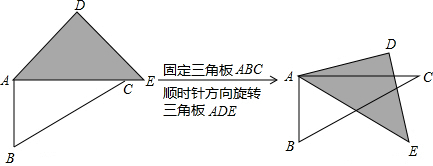
分析 要分5种情况进行讨论:AD∥BC、DE∥AB、DE∥BC、DE∥AC、AE∥BC分别画出图形,再分别计算出度数即可.
解答 解:当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的情况如下图所示:

①当AD∥BC时,α=15°;②当DE∥AB时,α=45°;③当DE∥BC时,α=105°;④当DE∥AC时,α=135°;⑤当AE∥BC时,α=150°.
故答案为:15°,45°,105°,135°,150°.
点评 本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度.

练习册系列答案
相关题目
1.化简$\frac{{a}^{2}}{a-1}+\frac{1}{1-a}$的结果是( )
| A. | a | B. | a+1 | C. | a-1 | D. | a2-1 |
14.下列式子一定是二次根式的是( )
| A. | $\sqrt{-2}$ | B. | $\sqrt{0.03}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-{x}^{2}-1}$ |
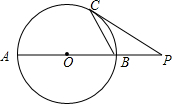 如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.
如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$. 如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.
如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.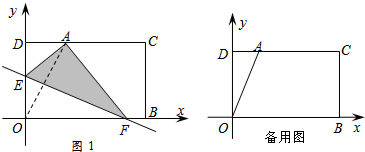
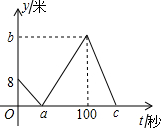 小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法:
小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法: