题目内容
12.已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点,若点M为第三象限内抛物线上一动点,△AMB的面积为S,则S的最大值为4.分析 根据待定系数法求得抛物线的解析式,然后过M作x轴垂线MN,三角形AMB面积=梯形MNOB面积+三角形AMN面积-三角形AOB面积,求出即可.
解答  解:设抛物线解析式为y=a(x+4)(x-2),
解:设抛物线解析式为y=a(x+4)(x-2),
将B(0,-4)代入得:-4=-8a,即a=$\frac{1}{2}$,
则抛物线解析式为y=$\frac{1}{2}$(x+4)(x-2)=$\frac{1}{2}$x2+x-4;
过M作MN⊥x轴,设M的横坐标为m,则M(m,$\frac{1}{2}$m2+m-4),
∴MN=|$\frac{1}{2}$m2+m-4|=-$\frac{1}{2}$m2-m+4,ON=-m,
∵A(-4,0),B(0,-4),∴OA=OB=4,
∴△AMB的面积为S=S△AMN+S梯形MNOB-S△AOB
=$\frac{1}{2}$×(4+m)×(-$\frac{1}{2}$m2-m+4)+$\frac{1}{2}$×(-m)×(-$\frac{1}{2}$m2-m+4+4)-$\frac{1}{2}$×4×4
=2(-$\frac{1}{2}$m2-m+4)-2m-8
=-m2-4m
=-(m+2)2+4,
当m=-2时,S取得最大值,最大值为4.
故答案为4.
点评 此题考查了二次函数综合题,涉及的知识有:待定系数法求抛物线解析式,坐标与图形性质,三角形及梯形的面积求法,以及二次函数的性质,熟练掌握二次函数的图象与性质是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
7.正比例函数y=2x的图象与反比例函数y=$\frac{3}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第一、三象限 | D. | 第二、四象限 |
17.化简$\frac{1}{x-1}+\frac{2}{1-{x}^{2}}$的结果是( )
| A. | x-1 | B. | $\frac{1}{x+1}$ | C. | x+1 | D. | $\frac{x+3}{{x}^{2}-1}$ |
1.化简$\frac{{a}^{2}}{a-1}+\frac{1}{1-a}$的结果是( )
| A. | a | B. | a+1 | C. | a-1 | D. | a2-1 |

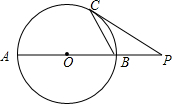 如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.
如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.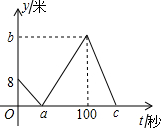 小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法:
小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法: