题目内容
7.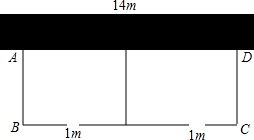 如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.
如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.
分析 利用长方形的面积÷宽=长求得AD即可,进一步利用竹篱总长为22m,可列分式方程,进一步代入数值验证即可.
解答 解:设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{22+1+1-3x}$=$\frac{45}{24-3x}$,
根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,
当x=5时,24-3x=9<14,符合题意;
当x=3时,24-3x=15>14,不符合题意.
故答案为:$\frac{45}{24-3x}$,$\frac{45}{24-3x}$+3x-2=22.
点评 此题考查分是方程的实际运用,利用长方形的面积计算公式建立方程是解决问题的关键.

练习册系列答案
相关题目
12.某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
2. 如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )
如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )
 如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )
如图所示,AH∥DG∥BC,DF∥AC,图中和∠ACB相等的角(不包括自身)有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
 如图所示,沿AE折叠矩形,点D恰好落在BC边上的点F处,已知AB=8cm,BC=10cm,求EC的长.
如图所示,沿AE折叠矩形,点D恰好落在BC边上的点F处,已知AB=8cm,BC=10cm,求EC的长. 如图,四边形ABCD是平行四边形,AE、CF分别与直线DB相交于点E和点F,且AE∥CF,分别连接点C、E和点A、F,求证:四边形AFCE是平行四边形.
如图,四边形ABCD是平行四边形,AE、CF分别与直线DB相交于点E和点F,且AE∥CF,分别连接点C、E和点A、F,求证:四边形AFCE是平行四边形.
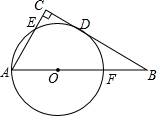 如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F. 如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是4.
如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是4.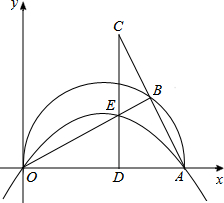 如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点.
如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点.