题目内容
12.某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 列表法或画树状图法可以不重复不遗漏地列出所有可能的结果,适合于两步完成的事件.
解答 解:列表:
| 第二次 第一次 | 0 | 10 | 20 | 30 |
| 0 | -- | 10 | 20 | 30 |
| 10 | 10 | -- | 30 | 40 |
| 20 | 20 | 30 | -- | 50 |
| 30 | 30 | 40 | 50 | -- |
因此P(不低于30元)=$\frac{8}{12}$=$\frac{2}{3}$.
故选:C.
点评 本题主要考查用列表法或树状图求概率.解决本题的关键是弄清题意,满200元可以摸两次,但摸出一个后不放回,概率在变化.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
2.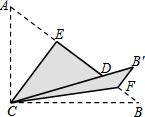 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
4.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
| A. | 60° | B. | 72° | C. | 90° | D. | 108° |
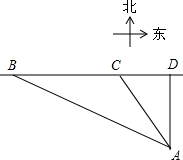 为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)
为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4) 如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )



 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为3.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为3.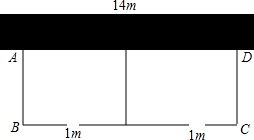 如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.
如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.